Sisällön pääryhmät Derivaatta Maksimit ja minimit [ 1 2 3 4 5 ] ESITIEDOT:  reaalifunktiot,  derivaatta KATSO MYÖS:  funktion jatkuvuus,  derivointisäännöt,  alkeisfunktioiden derivaatat

Kansisivu  Sisältö  Hakemisto

Funktion suurin ja pienin arvo eli absoluuttinen maksimi ja absoluuttinen minimi argumentin ollessa reaaliakselin suljetulla välillä löydetään etsimällä paikalliset ääriarvot ja tarkastelemalla funktion käyttäytymistä välin päätepisteissä. Edellytyksenä on, että funktio on välillä derivoituva (jolloin se on myös jatkuva). Menettely on seuraava:

1. Etsitään funktion derivaatan nollakohdat tarkasteluvälillä ja lasketaan vastaavat funktion arvot. Kaikki nollakohdat eivät välttämättä ole ääriarvokohtia, mutta tällä ei menettelyssä ole merkitystä. Myöskään ääriarvojen laatua (maksimi, minimi) ei tarvitse tutkia.
2. Lasketaan funktion arvot välin päätepisteissä.
3. Suurin saaduista arvoista on funktion maksimiarvo, pienin minimiarvo.

Jos tarkasteluväli on avoin, on lisäksi raja-arvotarkasteluilla tutkittava funktion käyttäytymistä lähestyttäessä välin päätepisteitä (tai äärettömyyttä, jos väli on rajoittamaton). Jos funktio ei joissakin pisteissä ole derivoituva tai edes jatkuva, on tutkittava raja-arvot myös näitä pisteitä lähestyttäessä.

Tällöin on mahdollista, että funktiolla ei ole maksimia tai minimiä, so. suurinta tai pienintä arvoa, jonka funktio saisi jossakin pisteessä. Sen sijaan voidaan ehkä löytää funktion arvoille pienin yläraja tai suurin alaraja, so. mahdollisimman ahtaat rajat, joiden välissä funktion arvot ovat. Toisena mahdollisuutena on, että funktio on rajoittamaton ylhäältä tai alhaalta, so. saa miten suuria tai miten pieniä arvoja tahansa. (Tällöin sanotaan, että funktion pienin yläraja on ja suurin alaraja -.)

On syytä huomata, että edellä olevaa menettelyä ei luonnollisestikaan tarvitse orjallisesti noudattaa, jos asia on pääteltävissä yksinkertaisemmin. Esimerkiksi funktion

f(x) =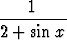

maksimi- ja minimiarvo reaaliakselilla ovat ilmeisestikin 1 ja 1/3, koska sinin pienin arvo on -1 (mikä vastaa funktion f suurinta arvoa) ja suurin arvo +1 (vastaten funktion f pienintä arvoa). Minkäänlainen derivointi ei siis tässä ole tarpeen.

suljettu väli  derivoituvuus  jatkuvuus  avoin väli  raja-arvo (funktion)  sini

Kivelä, niinkuin matematiikka, versio 1.12