![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Derivaatta
Derivaatta  Maksimit ja minimit [ 1 2 3
4 5 ]
Maksimit ja minimit [ 1 2 3
4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) derivaatta
derivaatta
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus,
funktion jatkuvuus, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt,
derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden
derivaatat
alkeisfunktioiden
derivaatat
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Derivaatta Derivaatta  Maksimit ja minimit [ 1 2 3
4 5 ] Maksimit ja minimit [ 1 2 3
4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) derivaatta derivaatta
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus, funktion jatkuvuus, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt, derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden
derivaatat alkeisfunktioiden
derivaatat
|
|
Olkoot x1, ..., xp positiivilukuja. Näiden aritmeettinen keskiarvo ja geometrinen keskiarvo ovat
Ma = 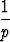  xk = xk = 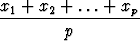 , , |
Mg =  = = 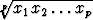 . . |
On osoitettava, että Ma > Mg ja että yhtäsuuruus esiintyy vain, kun kaikki luvut ovat yhtä suuria.
Tarkastellaan funktiota f(x) = x - ln x - 1, missä x > 0. Tämän derivaatta f'(x) = 1 - 1/x on = 0 pisteessä x = 1.
Koska limx 0+ ln x = -
0+ ln x = - ja standardiraja-arvona limx
ja standardiraja-arvona limx
 x - ln x =
x - ln x =
limx
 ln(ex/x) =
ln(ex/x) =  , ovat funktion raja-arvot tarkastelualueen päätepisteissä
, ovat funktion raja-arvot tarkastelualueen päätepisteissä
limx 0+f(x) = limx
0+f(x) = limx
 f(x) =
f(x) =  .
.
Piste x = 1 antaa siis funktion minimiarvon f(1) = 0, ts. x - ln x - 1 > 0 kaikilla x. Koska muita derivaatan nollakohtia ei ole, minimiarvo saadaan vain tässä pisteessä.
Sovelletaan saatua tulosta lukuihin xk/Ma ja lasketaan epäyhtälöt puolittain yhteen:
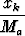 - ln
- ln 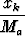 - 1 > 0, k = 1, ..., p,
- 1 > 0, k = 1, ..., p,
ja siis
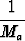
 xk - ln
xk - ln 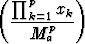 - p > 0.
- p > 0.
Lausumalla summa ja tulo keskiarvojen avulla sekä jakamalla luvulla p saadaan
- ln 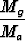 > 0,
> 0,
mistä seuraa Ma > Mg. Päättelyssä vallitsee yhtäsuuruus, jos alussa sovelletussa epäyhtälössä on x = 1 eli xk = Ma kaikilla indekseillä k; tämä merkitsee lukujen xk yhtäsuuruutta.
![[#]](kuvat/msam10-c-4.gif) keskiarvo (aritmeettinen) keskiarvo (aritmeettinen)![[#]](kuvat/msam10-c-4.gif) keskiarvo (geometrinen) keskiarvo (geometrinen)![[#]](kuvat/msam10-c-4.gif) logaritmifunktio logaritmifunktio![[#]](kuvat/msam10-c-4.gif) derivointi (alkeisfunktioiden) derivointi (alkeisfunktioiden)![[#]](kuvat/msam10-c-4.gif) raja-arvo (standardi-,
funktion) raja-arvo (standardi-,
funktion) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12