![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Derivaatta
Derivaatta  Maksimit ja minimit [ 1 2 3
4 5 ]
Maksimit ja minimit [ 1 2 3
4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) derivaatta
derivaatta
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus,
funktion jatkuvuus, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt,
derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden
derivaatat
alkeisfunktioiden
derivaatat
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Derivaatta Derivaatta  Maksimit ja minimit [ 1 2 3
4 5 ] Maksimit ja minimit [ 1 2 3
4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) derivaatta derivaatta
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus, funktion jatkuvuus, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt, derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden
derivaatat alkeisfunktioiden
derivaatat
|
|
Oletetaan seuraavassa, että funktio f on derivoituva ja että f'(x0) = 0. Oletetaan
lisäksi, että x0 on derivaatan erillinen nollakohta, ts. pisteellä x0 on ympäristö,
jossa f'(x)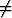 0 (paitsi tietenkin keskipisteessä x0).
0 (paitsi tietenkin keskipisteessä x0).
Kohtaa x0 ohitettaessa derivaatan merkki voi 1) muuttua positiivisesta negatiiviseksi, 2) negatiivisesta positiiviseksi, 3) jäädä muuttumatta.
Ensimmäisessä tapauksessa funktio muuttuu kasvavasta väheneväksi, jolloin kyseessä on maksimikohta; toisessa tapauksessa kyseessä on vastaavasti minimikohta. Jos merkki jää muuttumatta, on derivaatta samanmerkkinen pisteen x0 kummallakin puolella. Jos se on positiivinen, on funktio kasvava pisteen kummallakin puolella; jos negatiivinen, niin funktio on vähenevä. Kummassakaan tapauksessa ei kyseessä voi olla ääriarvokohta.
Ääriarvon laatu voidaan tutkia myös toista derivaattaa käyttäen. Olkoon f'(x0) = 0. Jos f''(x0) < 0, niin ensimmäinen derivaatta on kohdassa x0 vähenevä ja sen merkki siis muuttuu positiivisesta negatiiviseksi. Kyseessä on edellä olevan mukaan maksimi. Vastaavasti f''(x0) > 0 merkitsee, että kyseessä on minimi.
Jos f'(x0) = f''(x0) = 0, ei ääriarvon laatua tai sen olemassaoloa voida ilman lisätietoja päätellä. Kaikki on mahdollista. Esimerkiksi funktioilla x4, -x4 ja x3 on sekä ensimmäinen että toinen derivaatta origossa = 0. Ensimmäisellä on origossa minimi, toisella maksimi, kolmannella origo ei ole ääriarvokohta.
![[#]](kuvat/msam10-c-4.gif) derivaatta derivaatta![[#]](kuvat/msam10-c-4.gif) derivoituvuus derivoituvuus![[#]](kuvat/msam10-c-4.gif) kasvava (funktio) kasvava (funktio)![[#]](kuvat/msam10-c-4.gif) kasvava (funktio) kasvava (funktio)![[#]](kuvat/msam10-c-4.gif) vähenevä
(funktio) vähenevä
(funktio)![[#]](kuvat/msam10-c-4.gif) vähenevä (funktio) vähenevä (funktio)![[#]](kuvat/msam10-c-4.gif) derivaatta (toinen) derivaatta (toinen) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12