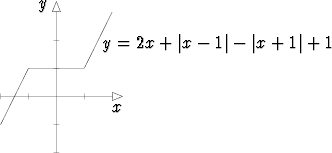Funktion kasvavuus ja vähenevyys
Reaalimuuttujan reaaliarvoista funktiota kutsutaan kasvavaksi, jos kaikilla
tarkastelujoukkoon kuuluvilla arvoilla x1, x2 pätee
x1 < x2 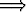 f(x1) < f(x2).
f(x1) < f(x2).
Jos funktionarvojen välillä ei sallita yhtäsuuruutta, funktio on aidosti
kasvava:
x1 < x2 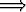 f(x1) < f(x2).
f(x1) < f(x2).
Ehdot
x1 < x2 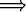 f(x1) > f(x2) ja f(x1) > f(x2) ja |
x1 < x2 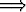 f(x1) > f(x2) f(x1) > f(x2) |
merkitsevät vastaavasti, että funktio on vähenevä ja aidosti vähenevä.
Terminologia ei ole aivan vakiintunutta. Eri yhteyksissä saatetaan (aidolle)
kasvavuudelle ja (aidolle) vähenevyydelle antaa hieman edellisestä poikkeaviakin
määrittelyjä. Voidaan myös käyttää toisenlaisia nimityksiä, esimerkiksi
ei-kasvava, ei-vähenevä. Syy on edellä olevien määritelmien hieman erikoisessa
piirteessä: Jos funktion arvo on vakio, kyseessä on sekä kasvava että vähenevä
funktio!
Esimerkkejä: Funktio f(x) = x3 on aidosti kasvava kaikkialla. Funktio
f(x) = 2x + |x - 1| - |x + 1| + 1 on kaikkialla kasvava, mutta ei aidosti kasvava,
koska se saa välillä [-1, 1] vakioarvon 1.
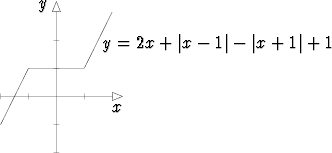
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Funktio
Funktio  Reaalifunktiot [ 1 2 3 4 5
]
Reaalifunktiot [ 1 2 3 4 5
]
![[#]](kuvat/msam10-c-4.gif) funktiokäsite
funktiokäsite
![[#]](kuvat/msam10-c-4.gif) potenssi,
potenssi, ![[#]](kuvat/msam10-c-4.gif) juuret,
juuret, ![[#]](kuvat/msam10-c-4.gif) polynomit,
polynomit, ![[#]](kuvat/msam10-c-4.gif) rationaalifunktiot,
rationaalifunktiot,
![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio,
eksponenttifunktio, ![[#]](kuvat/msam10-c-4.gif) logaritmifunktio,
logaritmifunktio, ![[#]](kuvat/msam10-c-4.gif) trigonometriset funktiot,
trigonometriset funktiot, ![[#]](kuvat/msam10-c-4.gif) arcus-funktiot,
arcus-funktiot,
![[#]](kuvat/msam10-c-4.gif) hyperbelifunktiot,
hyperbelifunktiot, ![[#]](kuvat/msam10-c-4.gif) area-funktiot
area-funktiot
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto