![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Area-funktiot [ 1 2 3
]
Area-funktiot [ 1 2 3
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) hyperbelifunktiot,
hyperbelifunktiot, ![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio,
eksponenttifunktio,
![[#]](kuvat/msam10-c-4.gif) logaritmifunktio
logaritmifunktio
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) arcus-funktiot
arcus-funktiot
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Area-funktiot [ 1 2 3
] Area-funktiot [ 1 2 3
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) hyperbelifunktiot, hyperbelifunktiot, ![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio, eksponenttifunktio,
![[#]](kuvat/msam10-c-4.gif) logaritmifunktio logaritmifunktio
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) arcus-funktiot arcus-funktiot
|
|
Hyperbelisini on aidosti kasvava funktio 

 . Sillä on tällöin käänteisfunktio
. Sillä on tällöin käänteisfunktio


 . Tätä merkitään arsinh; luetaan yleensä latinan tapaan area sinus
hyperbolicus. Siis:
. Tätä merkitään arsinh; luetaan yleensä latinan tapaan area sinus
hyperbolicus. Siis:
y = arsinh x 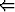
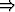 x = sinh y.
x = sinh y.
Hyperbelikosini on aidosti kasvava bijektio vain, jos sen määrittelyaluetta
sopivasti rajoitetaan: [0,  [
[  [1,
[1,  [. Tällöin sillä on käänteisfunktio area cosinus
hyperbolicus arcosh : [1,
[. Tällöin sillä on käänteisfunktio area cosinus
hyperbolicus arcosh : [1,  [
[  [0,
[0,  [,
[,
y = arcosh x 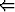
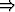 x = cosh y.
x = cosh y.
Määrittelyalue voitaisiin yhtä hyvin rajoittaa funktion aidosti vähenevään osaan:
] -  , 0]
, 0]  [1,
[1,  [. Tätä vastaten saadaan myös käänteisfunktio, jota
kutsutaan funktion sivuhaaraksi. Sen arvot ovat päähaara-arvojen vastalukuja:
- arcosh x.
[. Tätä vastaten saadaan myös käänteisfunktio, jota
kutsutaan funktion sivuhaaraksi. Sen arvot ovat päähaara-arvojen vastalukuja:
- arcosh x.
Hyperbelitangentti on aidosti kasvava bijektio 
 ] - 1, 1[, jolloin sillä on
käänteisfunktio artanh :] - 1, 1[
] - 1, 1[, jolloin sillä on
käänteisfunktio artanh :] - 1, 1[ 
 ,
,
y = artanh x 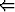
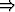 x = tanh y.
x = tanh y.
Vastaavaan tapaan voidaan menetellä myös hyperbelikotangentin suhteen.
Nimitys area tarkoittaa erästä pinta-alaa; vrt. hyperbolisten ja trigonometristen funktioiden vertailuun. Tämän johdosta funktionnimien alkuosan tuleekin olla ar eikä arc, vaikka jälkimmäistäkin toisinaan näkee. Minkään kaaren (arcus) pituuteen ei funktioiden arvoja nimittäin voida luonnollisella tavalla liittää.
![[#]](kuvat/msam10-c-4.gif) kasvava (funktio) kasvava (funktio)![[#]](kuvat/msam10-c-4.gif) kasvava (funktio) kasvava (funktio)![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio![[#]](kuvat/msam10-c-4.gif) bijektio bijektio![[#]](kuvat/msam10-c-4.gif) vähenevä (funktio) vähenevä (funktio)![[#]](kuvat/msam10-c-4.gif) vähenevä (funktio) vähenevä (funktio)![[#]](kuvat/msam10-c-4.gif) hyperbeli- ja trigonometriset funktiot hyperbeli- ja trigonometriset funktiot |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12