Sisällön pääryhmät Alkeisfunktiot Hyperbelifunktiot [ 1 2 3 4 ] ESITIEDOT:  reaalifunktiot,  eksponenttifunktio KATSO MYÖS:  trigonometriset funktiot,  trigonometrian kaavat

Kansisivu  Sisältö  Hakemisto

Hyperbelifunktioiden ja trigonometristen funktioiden välillä vallitsee tietynlainen samankaltaisuus. Tämä näkyy mm. funktioita koskevista kaavoista. Sama koskee funktioiden derivaattoja. Erojakin kuitenkin on. Hyperbelifunktiot esimerkiksi eivät ole jaksollisia. Hyperbelifunktioiden ja trigonometristen funktioiden sukulaisuus tulee täysin ilmeiseksi vasta laajennettaessa funktioiden määrittely kompleksitasoon. Tällöin hyperbelifunktioistakin tulee jaksollisia. Lähemmin ei asiaa tässä käsitellä.

Hieman epämääräisesti voidaan sanoa, että hyperbelifunktiot suhtautuvat tasasivuiseen hyperbeliin x² - y² = 1 samaan tapaan, kuin trigonometriset funktiot suhtautuvat yksikköympyrään x² + y² = 1.

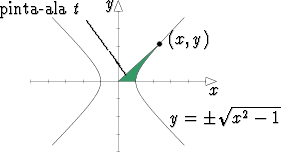
Jos origo yhdistetään hyperbelin pisteeseen (x, y) ja yhdysjanan, hyperbelinkaaren ja x-akselin rajaamaa pinta-alaa merkitään t, niin x = cosh(2t), y = sinh(2t). Tämä on osoitettavissa integraalilaskennan avulla.

Vastaava tulos on voimassa myös trigonometrisella puolella: Koska yksikköympyrän keskuskulmaa vastaavan sektorin ala on t = 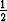, on x = cos(2t), y = sin(2t).

trigonometrinen funktio (yleinen määritelmä)  derivaatta  jaksollinen (funktio)  kompleksitaso  hyperbeli (kartioleikkauksena)  hyperbeli (xy-koordinaateissa)  määrätty integraali  keskuskulma  sektori  sektori (ala)

Kivelä, niinkuin matematiikka, versio 1.12