Sisällön pääryhmät Luvut Reaaliluvut [ 1 2 3 4 5 6 7 ] ESITIEDOT: KATSO MYÖS:  murtoluvut,  lukujärjestelmät,  kompleksiluvut

Kansisivu  Sisältö  Hakemisto

Reaaliluvut voidaan jaotella myös seuraavasti: Jos luku on jonkin kokonaislukukertoimisen polynomiyhtälön juuri, sitä sanotaan algebralliseksi luvuksi. Jos näin ei ole, kyseessä on transkendenttiluku.

Esimerkiksi on transkendenttiluku. Algebrallisia lukuja ovat mm. kaikki rationaaliluvut ja neliöjuuret, kuutiojuuret, jne. Vaikkapa 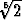on algebrallinen luku, koska se toteuttaa yhtälön x⁵ - 2 = 0. Ensimmäisen asteen yhtälön 197x = 31 juuri on 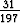, joten sekin on algebrallinen luku. Algebrallisia lukuja on kuitenkin muitakin, koska läheskään kaikkien polynomiyhtälöiden juuria ei voida lausua juurilausekkeina.

Ks. korkeamman asteen yhtälöt.

yhtälö (polynomi-)  juuri (polynomin)  pii  pii (sarja)  yhtälö (korkeamman asteen)

Kivelä, niinkuin matematiikka, versio 1.12