Sisällön pääryhmät Yhtälöt ja epäyhtälöt Polynomiyhtälöt [ 1 2 3 ] ESITIEDOT:  yhtälöt,  polynomit,  juuret KATSO MYÖS:  Newtonin iteraatio,  polynomien tekijöihin jako,  kompleksiluvut

Kansisivu  Sisältö  Hakemisto

Polynomiyhtälöt jaotellaan polynomin asteluvun mukaan.

Ensimmäisen asteen polynomiyhtälö, lyhyemmin ensimmäisen asteen yhtälö on muotoa ax + b = 0, missä a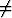0. Ratkaisuja on yksi: x = -b/a.

Toisen asteen yhtälö on muotoa ax² + bx + c = 0, missä a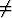0. Yhtälö ratkaistaan yleensä ulkoa opituilla ratkaisukaavoilla:

x = .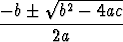

Jos yhtälö jaetaan kertoimella a, se saa periaatteessa muodon x² + px + q = 0. Ratkaisukaavat esitetään usein myös tätä tapausta varten:

x = - ± .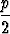

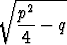Vastaten ratkaisukaavojen ±-merkkiä, juuria on yleensä kaksi. Näiden luonteen ratkaisee diskriminantti, so. neliöjuurimerkin alla oleva lauseke D = b² - 4ac.

Jos yhtälö on reaalikertoiminen, saadaan seuraavat tapaukset: Jos D > 0, yhtälöllä on kaksi eri suurta reaalista juurta. Jos D = 0, sanotaan juurien yhtyvän, ts. on vain yksi reaalijuuri x = -b/(2a). Jos D < 0, juurina on kompleksinen liittolukupari. Toisen asteen yhtälö voi olla myös kompleksikertoiminen, so. kertoimet a, b ja c tai jotkut niistä voivat olla kompleksilukuja. Samat ratkaisukaavat ovat tällöinkin käytettävissä, mutta neliöjuurimerkin alle saadaan yleensä kompleksiluku ja juuren laskeminen edellyttää laajempaa perehtyneisyyttä kompleksilukuihin.

yhtälö  polynomi  asteluku  neliöjuuri  kompleksiluku  liittoluku

Kivelä, niinkuin matematiikka, versio 1.12