![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Potenssit ja polynomit
Potenssit ja polynomit  Polynomien
tekijöihin jako [ 1 2 3 4 ]
Polynomien
tekijöihin jako [ 1 2 3 4 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) polynomit,
polynomit, ![[#]](kuvat/msam10-c-4.gif) reaaliluvut,
reaaliluvut, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut
kompleksiluvut
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt
polynomiyhtälöt
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Potenssit ja polynomit Potenssit ja polynomit  Polynomien
tekijöihin jako [ 1 2 3 4 ] Polynomien
tekijöihin jako [ 1 2 3 4 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) polynomit, polynomit, ![[#]](kuvat/msam10-c-4.gif) reaaliluvut, reaaliluvut, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut kompleksiluvut
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt polynomiyhtälöt
|
|
Polynomien tekijöihin jako on usein tarvittava apukeino. Tärkeitä peruskaavoja ovat seuraavat:
| x2 - y2 | = | (x - y)(x + y), | ||
| xn - yn | = | (x - y)(xn-1 + xn-2y + xn-3y2 + ... + xyn-2 + yn-1) |
xn + yn = (x + y)(xn-1 - xn-2y + xn-3y2 - ... - xyn-2 + yn-1).
Lisäksi polynomien tekijöihin jaossa voidaan käyttää binomikaavaa (Pascalin kolmiota) tai multinomikaavaa käänteiseen suuntaan.
Polynomin tekijöihin jakoa tarvitaan usein lausekkeiden sieventämisessä. Tällöin eo. kaavoja joudutaan käyttämään molempiin suuntiin. Sieventämisen tavoite ei yleensä ole itsestään selvä, vaan se riippuu yhteydestä: mitä lausekkeelle on seuraavaksi tarkoitus tehdä. Esimerkiksi ei ole selvää, kumpaa seuraavista muodoista on pidettävä sievempänä:
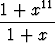 = 1 - x + x2 - x3 + x4 - x5 + x6 - x7 + x8 - x9 + x10.
= 1 - x + x2 - x3 + x4 - x5 + x6 - x7 + x8 - x9 + x10.
![[#]](kuvat/msam10-c-4.gif) binomikaava binomikaava![[#]](kuvat/msam10-c-4.gif) binomikaava binomikaava![[#]](kuvat/msam10-c-4.gif) Pascalin kolmio Pascalin kolmio![[#]](kuvat/msam10-c-4.gif) multinomikaava multinomikaava![[#]](kuvat/msam10-c-4.gif) multinomikaava multinomikaava |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12