![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Luvut
Luvut  Kompleksiluvut [ 1 2 3 4 5 6
]
Kompleksiluvut [ 1 2 3 4 5 6
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaaliluvut
reaaliluvut
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) polynomien tekijöihin jako,
polynomien tekijöihin jako, ![[#]](kuvat/msam10-c-4.gif) vektori
vektori
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Luvut Luvut  Kompleksiluvut [ 1 2 3 4 5 6
] Kompleksiluvut [ 1 2 3 4 5 6
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaaliluvut reaaliluvut
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) polynomien tekijöihin jako, polynomien tekijöihin jako, ![[#]](kuvat/msam10-c-4.gif) vektori vektori
|
|
Kompleksiluvun z = x + iy napakulma eli argumentti  on pisteen (x, y)
suuntakulma positiiviseen x-akseliin nähden; tämä valitaan yleensä väliltä
] -
on pisteen (x, y)
suuntakulma positiiviseen x-akseliin nähden; tämä valitaan yleensä väliltä
] -  ,
,  ].
].
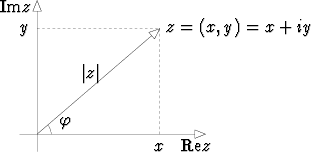
Koska napakoordinaateille pätee trigonometristen funktioiden määritelmien mukaan
x = r cos  , y = r sin
, y = r sin  , missä r =
, missä r = 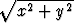 = |z|, saadaan kompleksiluvulle
napakoordinaattiesitys
= |z|, saadaan kompleksiluvulle
napakoordinaattiesitys
z = x + yi = |z|(cos  + i sin
+ i sin  ).
).
Tämän avulla voidaan myös kompleksilukujen kertolasku luonnehtia geometrisesti:
Olkoon kerrottavana kompleksiluvut
z1 = |z1|(cos  1 + i sin
1 + i sin  1), z2 = |z2|(cos
1), z2 = |z2|(cos  2 + i sin
2 + i sin  2).
2).
Näiden tulo on
| z1z2 | = | |z1||z2| [(cos  1 cos 1 cos  2 - sin 2 - sin  1 sin 1 sin  2) 2) | ||
+i(cos  1 sin 1 sin  2 + sin 2 + sin  1 cos 1 cos  2)] 2)] | ||||
| = | |z1||z2| [cos( 1 + 1 +  2) + i sin( 2) + i sin( 1 + 1 +  2)], 2)], |
![[#]](kuvat/msam10-c-4.gif) suuntakulma (suoran) suuntakulma (suoran)![[#]](kuvat/msam10-c-4.gif) väli (reaaliakselin) väli (reaaliakselin)![[#]](kuvat/msam10-c-4.gif) napakoordinaatit (kompleksitason) napakoordinaatit (kompleksitason)![[#]](kuvat/msam10-c-4.gif) napakoordinaatit (tason) napakoordinaatit (tason)![[#]](kuvat/msam10-c-4.gif) trigonometrinen funktio (yleinen määritelmä) trigonometrinen funktio (yleinen määritelmä)![[#]](kuvat/msam10-c-4.gif) trigonometria (peruskaavat) trigonometria (peruskaavat) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12