Sisällön pääryhmät Geometrian peruskäsitteet Suora [ 1 2 3 4 5 ] ESITIEDOT:  vektori,  koordinaatistot,  piste KATSO MYÖS:  geometria,  vektorialgebra,  geometriset probleemat,  taso

Kansisivu  Sisältö  Hakemisto

Tarkastellaan suoran yhtälöä ax + by + c = 0 tavallisessa xy-tasossa. Jos b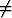0, tästä voidaan ratkaista y:

y = -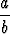 x - .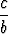

Muuttujan x kerroin -a/b on suoran kulmakerroin, joka kuvaa sen kaltevuutta. Vakiotermi -c/b osoittaa, missä pisteessä suora leikkaa y-akselin.

Jos b = 0, on suoran yhtälö ax + c = 0 eli x = -c/a. Tällöin se on y-akselin suuntainen. Tällaisen suoran yhtälöä ei voida ratkaista y:n suhteen, so. saattaa muotoon y = kx + p.

Suoran ja x-akselin positiivisen suunnan välistä kulmaa kutsutaan suoran suuntakulmaksi. Tämä valitaan aina väliltä ] - 90^o, 90^o]. Arvo 90^o vastaa y-akselin suuntaista suoraa.

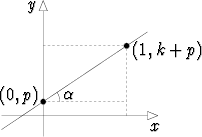
Jos suoran yhtälössä y = kx + p asetetaan x = 0, on y = p; vastaavasti jos x = 1, niin y = k + p. Alla olevan kuvion perusteella on tällöin k = tan , ts. kulmakerroin on suuntakulman tangentti. Jos suora on nouseva, kulmakerroin on positiivinen; laskevalla suoralla se on negatiivinen.

koordinaatisto (xy-)  väli (reaaliakselin)  tangentti (trigonometrinen)

Kivelä, niinkuin matematiikka, versio 1.12