![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometrian peruskäsitteet
Geometrian peruskäsitteet  Suora [ 1 2 3
4 5 ]
Suora [ 1 2 3
4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) vektori,
vektori, ![[#]](kuvat/msam10-c-4.gif) koordinaatistot,
koordinaatistot, ![[#]](kuvat/msam10-c-4.gif) piste
piste
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) geometria,
geometria, ![[#]](kuvat/msam10-c-4.gif) vektorialgebra,
vektorialgebra, ![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat,
![[#]](kuvat/msam10-c-4.gif) taso
taso
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Geometrian peruskäsitteet Geometrian peruskäsitteet  Suora [ 1 2 3
4 5 ] Suora [ 1 2 3
4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) vektori, vektori, ![[#]](kuvat/msam10-c-4.gif) koordinaatistot, koordinaatistot, ![[#]](kuvat/msam10-c-4.gif) piste piste
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) geometria, geometria, ![[#]](kuvat/msam10-c-4.gif) vektorialgebra, vektorialgebra, ![[#]](kuvat/msam10-c-4.gif) geometriset probleemat, geometriset probleemat,
![[#]](kuvat/msam10-c-4.gif) taso taso
|
|
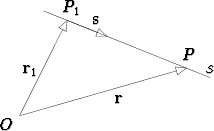
Olkoon annettuna kaksi tason tai avaruuden pistettä paikkavektoreidensa avulla:
P1  r1, P2
r1, P2  r2. Nämä määräävät yksikäsitteisesti suoran s.
r2. Nämä määräävät yksikäsitteisesti suoran s.
Vektori s = r2 - r1 on suoran s suuntainen; sitä kutsutaan suoran suuntavektoriksi.
Jos P  r on mikä tahansa suoran s piste, sen paikkavektori voidaan kirjoittaa
muotoon r = r1 + a s, kun skalaari a valitaan sopivasti. Toisaalta jos a on mikä
tahansa reaaliluku, antaa eo. lauseke aina jonkin suoralla s olevan pisteen
paikkavektorin.
r on mikä tahansa suoran s piste, sen paikkavektori voidaan kirjoittaa
muotoon r = r1 + a s, kun skalaari a valitaan sopivasti. Toisaalta jos a on mikä
tahansa reaaliluku, antaa eo. lauseke aina jonkin suoralla s olevan pisteen
paikkavektorin.
Tämän johdosta sanotaankin, että
r = r1 + a s, a 
 ,
,
on suoran s vektoriesitys. Luku a on parametri, jota vaihtelemalla saadaan kaikki suoran pisteet.
Suuntavektori s ei ole yksikäsitteinen, vaan mikä tahansa suoran suuntainen vektori kelpaa. Myöskään paikkavektori r1 ei ole yksikäsitteinen. Tämä merkitsee, että samalle suoralle saadaan useita erilaisia vektoriesityksiä.
Suorien vektoriesitykset mahdollistavat vektorialgebran käytön geometrian menetelmänä.
![[#]](kuvat/msam10-c-4.gif) vektori vektori![[#]](kuvat/msam10-c-4.gif) paikkavektori paikkavektori![[#]](kuvat/msam10-c-4.gif) skalaari skalaari![[#]](kuvat/msam10-c-4.gif) geometria (vektori-) geometria (vektori-) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12