Sisällön pääryhmät Luvut Kompleksiluvut [ 1 2 3 4 5 6 ] ESITIEDOT:  reaaliluvut KATSO MYÖS:  polynomien tekijöihin jako,  vektori

Kansisivu  Sisältö  Hakemisto

Kompleksilukujoukko muodostuu kompleksiluvuista (x, y), ts. xy-tason pisteistä. Reaaliakselin — x-akselin — yksikköpiste on (1, 0); tämä vastaa reaalilukua 1, ts. 1 = (1, 0). Vastaavalla tavalla merkitään imaginaariakselin, y-akselin yksikköä eli imaginaariyksikköä i = (0, 1).

Kompleksiluvuille halutaan tavanomainen algebra — laskutoimitukset — jolloin on määriteltävä, miten niitä lasketaan yhteen, vähennetään, kerrotaan ja jaetaan keskenään. Tavoitteena on lisäksi, että tavanomaiset laskusäännöt ovat voimassa ja että i² = -1, jolloin ainakin yhtälölle x² + 1 = 0 on ratkaisu olemassa.

Yhteenlasku on luonnollista määritellä vektoriyhteenlaskuna:

(x₁, y₁) + (x₂, y₂) = (x₁ + x₂,  y₁ + y₂).

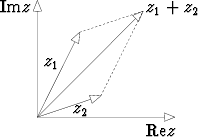
Vähennyslaskun määrittely tehdään samaan tapaan:

(x₁, y₁) - (x₂, y₂) = (x₁ - x₂,  y₁ - y₂).

Yhteenlaskun määrittelyn jälkeen on luonnollista kirjoittaa vektorialgebran tapaan (x, y) = (x, 0) + (0, y) = x(1, 0) + y(0, 1) = x + yi, jolloin on saatu kompleksiluvulle uusi esitysmuoto x + yi.

koordinaatisto (xy-)  reaaliluku  yhteenlasku (vektorien)

Kivelä, niinkuin matematiikka, versio 1.12