![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometrian peruskäsitteet
Geometrian peruskäsitteet  Vektori [ 1 2
3 ]
Vektori [ 1 2
3 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) koordinaatistot
koordinaatistot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) vektorialgebra
vektorialgebra
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Geometrian peruskäsitteet Geometrian peruskäsitteet  Vektori [ 1 2
3 ] Vektori [ 1 2
3 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) koordinaatistot koordinaatistot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) vektorialgebra vektorialgebra
|
|
Kaksi tason tai avaruuden vektoria a ja b lasketaan yhteen siten, että niiden suuntajanat asetetaan alkamaan samasta pisteestä ja summavektorin a + b edustajana oleva suuntajana muodostetaan syntyvän suunnikkaan lävistäjänä oheisen kuvion mukaisesti:
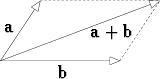
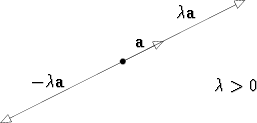
Vektori a kerrotaan skalaarilla eli reaaliluvulla 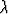 siten, että sen pituus kerrotaan
itseisarvolla |
siten, että sen pituus kerrotaan
itseisarvolla |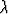 | ja suunta säilyy samana, jos
| ja suunta säilyy samana, jos 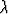 > 0, tai kääntyy vastakkaiseksi, jos
> 0, tai kääntyy vastakkaiseksi, jos
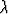 < 0. Jos
< 0. Jos 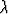 = 0, tuloksena on nollavektori. Vektorin a skalaarikerrannaista
merkitään
= 0, tuloksena on nollavektori. Vektorin a skalaarikerrannaista
merkitään 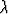 a.
a.
Vektoreiden yhteenlasku ja skalaarilla kertominen noudattavat kaikkia tavanomaisia laskusääntöjä: Yhteenlasku on vaihdannaista ja liitännäistä, ts. laskettaessa yhteen useita vektoreita ei järjestyksellä tai vektoreiden ryhmittelyllä (sulkujen käytöllä) ole merkitystä. Skalaarilla kertominen noudattaa osittelulakeja, jne.
![[#]](kuvat/msam10-c-4.gif) yhteenlasku (yleensä) yhteenlasku (yleensä)![[#]](kuvat/msam10-c-4.gif) kertolasku (yleensä) kertolasku (yleensä)![[#]](kuvat/msam10-c-4.gif) vaihdannaisuus vaihdannaisuus![[#]](kuvat/msam10-c-4.gif) liitännäisyys liitännäisyys![[#]](kuvat/msam10-c-4.gif) osittelulaki osittelulaki |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12