![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometrian peruskäsitteet
Geometrian peruskäsitteet  Vektori [ 1 2
3 ]
Vektori [ 1 2
3 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) koordinaatistot
koordinaatistot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) vektorialgebra
vektorialgebra
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Geometrian peruskäsitteet Geometrian peruskäsitteet  Vektori [ 1 2
3 ] Vektori [ 1 2
3 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) koordinaatistot koordinaatistot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) vektorialgebra vektorialgebra
|
|
Suorakulmaisen xy-koordinaatiston tai avaruudessa xyz-koordinaatiston koordinaattiakseleiden positiiviseen suuntaan osoittavia yksikkövektoreita kutsutaan kantavektoreiksi. Nämä ovat siis pituudeltaan = 1 ja toisiaan vastaan kohtisuoria. Kantavektoreiden symboleina käytetään i, j ja avaruudessa lisäksi k.
Yhteenlasku ja skalaarilla kertominen mahdollistavat vektorien jakamisen koordinaattiakseleiden suuntaisiin komponentteihin. Esimerkiksi pisteestä P = (2, -3, 1) alkava ja pisteeseen Q = (5, -5, 2) päättyvä suuntajana määrää vektorin, joka voidaan lausua summana kantavektoreiden suuntaisista komponenteista:
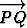 = 3i - 2j + k.
= 3i - 2j + k.
Komponentit voivat luonnollisesti olla muunkinlaisia kuin koordinaattiakseleiden suuntaisia. Esimerkiksi fysikaalisessa sovelluksessa, jossa tarkastellaan kaltevalla tasolla olevaa kappaletta, on voimavektorit luonnollista jakaa tason suuntaisiin ja sitä vastaan kohtisuoriin komponentteihin.
Muotoa
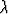 1a1 +
1a1 + 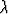 2a2 +
2a2 + 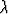 3a3
3a3
olevaa lauseketta kutsutaan vektoreiden a1, a2, a3 lineaariyhdistelyksi.
![[#]](kuvat/msam10-c-4.gif) koordinaatisto (xy-) koordinaatisto (xy-)![[#]](kuvat/msam10-c-4.gif) koordinaatisto (xyz-) koordinaatisto (xyz-)![[#]](kuvat/msam10-c-4.gif) piste piste |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12