![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Joukko-oppi [ 1
2 3 4 ]
Joukko-oppi [ 1
2 3 4 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) logiikka,
logiikka, ![[#]](kuvat/msam10-c-4.gif) reaaliluvut
reaaliluvut
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Joukko-oppi [ 1
2 3 4 ] Joukko-oppi [ 1
2 3 4 ]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) logiikka, logiikka, ![[#]](kuvat/msam10-c-4.gif) reaaliluvut reaaliluvut
|
|
Joukon A sanotaan olevan joukon B osajoukko, merkitään A 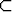 B, jos
jokainen joukon A alkio on myös joukon B alkio, ts. logiikan merkinnöin
x
B, jos
jokainen joukon A alkio on myös joukon B alkio, ts. logiikan merkinnöin
x  A
A 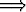 x
x  B.
B.
Merkintää A 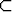 B käytettäessä on myös mahdollista, että joukot A ja B
ovat samat eli A = B. Jos erityisesti halutaan osoittaa, että A on aito
osajoukko, ts. on olemassa ainakin yksi alkio x siten, että x
B käytettäessä on myös mahdollista, että joukot A ja B
ovat samat eli A = B. Jos erityisesti halutaan osoittaa, että A on aito
osajoukko, ts. on olemassa ainakin yksi alkio x siten, että x  B ja x
B ja x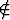 A,
merkitään usein A
A,
merkitään usein A 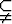 B. Näiltä osin merkinnät eivät kuitenkaan ole täysin
vakiintuneita.
B. Näiltä osin merkinnät eivät kuitenkaan ole täysin
vakiintuneita.
Tyhjän joukon katsotaan olevan minkä tahansa joukon osajoukko: Ø 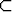 A.
A.
Esimerkiksi: Jos joukko F muodostuu kaikista funktioista 

 , joukko C0
jatkuvista ja C1 derivoituvista funktioista
, joukko C0
jatkuvista ja C1 derivoituvista funktioista 

 , niin C1
, niin C1 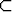 C0
C0 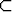 F , koska
jokainen derivoituva funktio on myös jatkuva. Kummassakin tapauksessa
osajoukko on aito.
F , koska
jokainen derivoituva funktio on myös jatkuva. Kummassakin tapauksessa
osajoukko on aito.
![[#]](kuvat/msam10-c-4.gif) logiikka logiikka![[#]](kuvat/msam10-c-4.gif) jatkuvuus jatkuvuus![[#]](kuvat/msam10-c-4.gif) derivoituvuus derivoituvuus |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12