![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Joukko-oppi [ 1
2 3 4 ]
Joukko-oppi [ 1
2 3 4 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) logiikka,
logiikka, ![[#]](kuvat/msam10-c-4.gif) reaaliluvut
reaaliluvut
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Joukko-oppi [ 1
2 3 4 ] Joukko-oppi [ 1
2 3 4 ]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) logiikka, logiikka, ![[#]](kuvat/msam10-c-4.gif) reaaliluvut reaaliluvut
|
|
Seuraavat eri joukkojen väliset suhteet tai operaatiot edellyttävät, että puhe on saman perusjoukon joukoista.
Joukkojen A ja B leikkaus muodostuu niiden yhteisestä osasta:
A 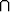 B = {x | x
B = {x | x  A ja x
A ja x  B}.
B}.
Tämä voi luonnollisesti olla tyhjä joukko.

Joukkojen A ja B unioniin kuuluvat molempien joukkojen alkiot:
A 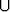 B = {x | x
B = {x | x  A tai x
A tai x  B}.
B}.
Erityisesti on siis A 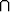 B
B 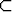 A
A 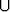 B.
B.
Joukon A komplementti (perusjoukon suhteen) muodostuu joukkoon A kuulumattomista alkioista:
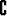 A = {x | x
A = {x | x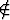 A}.
A}.
Joukon A komplementti joukon B suhteen on
B A = {x | x
A = {x | x  B ja x
B ja x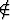 A}.
A}.

Kuvatut operaatiot voidaan ymmärtää joukkojen välisiksi laskutoimituksiksi. Näillä on omat laskusääntönsä, esimerkiksi:
A 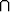 (B (B 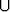 C) = (A C) = (A 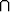 B) B) 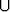 (A (A 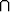 C), C), | |||
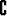 (A (A 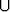 B) = ( B) = (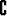 A) A) 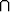 ( (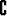 B), B), | |||
(A 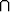 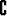 B) B) 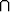 ( (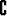 C) = A C) = A 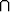 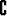 (B (B 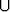 C). C). |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12