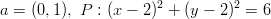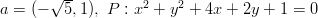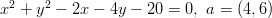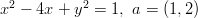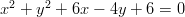Käyrät ja pinnat

xy-tason käyrä voidaan periaatteessa määritellä kahdella tavalla — joko koordinaatteja x ja y sitovana yhtälönä tai parametriesityksenä, jolloin kumpikin koordinaatti esitetään funktiona käyräparametrista. Jokaista parametrin arvoa vastaa tällöin käyrän piste (x,y).
xyz-avaruudessa käyrää vastaa pinta. Tällöin esityksenä voi olla koordinaatteja x, y ja z sitova yhtälö. Vaihtoehtona on parametriesitys, jossa kukin koordinaatti esitetään funktiona kahdesta parametrista.
Yksinkertaisin käyrä on ympyrä ja yksinkertaisin pinta pallo.
Toisen asteen käyräksi kutsutaan käyrää, jonka yhtälö koordinaattien x ja y suhteen on toista astetta. Ympyrä on tällainen käyrä. Muita toisen asteen käyriä ovat ellipsi, hyperbeli ja paraabeli. Ympyrä on ellipsin erikoistapaus. Näitä käyriä kutsutaan usein kartioleikkauksiksi, koska ne syntyvät kartiopinnan tasoleikkauksina.

Esimerkkejä
- Määritetään ympyrän yhtälö kun ympyrän keskipiste on
 ja säde
ja säde  .
.
Ympyrän yhtälö on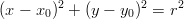 , missä
, missä 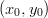 on keskipiste ja
on keskipiste ja  säde. Sijoitetaan arvot kaavaan
säde. Sijoitetaan arvot kaavaan

- Määritetään pisteiden
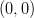 ,
,  ja
ja  kautta kulkevan
ympyrän yhtälö.
kautta kulkevan
ympyrän yhtälö.
Muodostetaan yhtälöryhmä käyttäen ympyrän kaavaa:
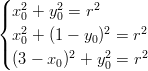
Aloitetaan yhtälöryhmän ratkaisu merkitsemällä kahden ensimmäisen lausekkeen vasemmat puolet samoiksi ja ratkaisemalla siitä
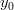 :
:
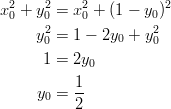
Ratkaistaan vastaavasti
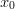 :
:

Ympyrän keskipiste on siis
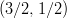 . Ratkaistaan säde
. Ratkaistaan säde  ensimmäisestä yhtälöstä:
ensimmäisestä yhtälöstä:

Kysytyn ympyrän yhtälö on
 .
.
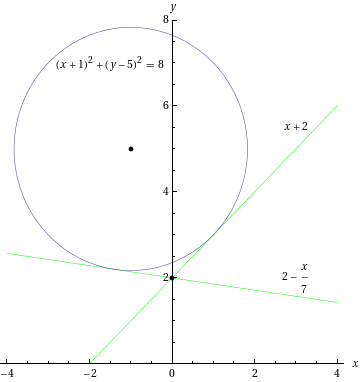
- Etsitään ympyrälle
 pisteen
pisteen 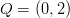 kautta
kulkeva tangentti.
kautta
kulkeva tangentti.
Ympyrän säde on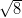 . Pisteen
. Pisteen  etäisyys ympyrän keskipisteestä
etäisyys ympyrän keskipisteestä
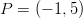 on
on
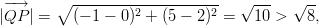
eli piste
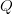 on ympyrän ulkopuolella. Pisteen
on ympyrän ulkopuolella. Pisteen  kautta kulkeva
tangentti on muotoa:
kautta kulkeva
tangentti on muotoa:
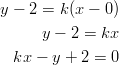
Muodostetaan yhtälö käyttäen tietoa, että tangentin ja ympyrän keskipisteen etäisyys on lyhyimmillään säteen
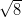 verran.
verran.
Pisteen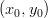 etäisyys suorasta
etäisyys suorasta  saadaan
kaavalla
saadaan
kaavalla
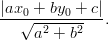

Tangenttien yhtälöt ovat

- Selvitetään pallon
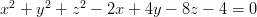 säde ja
keskipiste muuttamalla se ensin keskipistemuotoon.
säde ja
keskipiste muuttamalla se ensin keskipistemuotoon.
Järjestellään termejä uudelleen ja käytetään neliöksi täydentämistä:

Saadusta keskipistemuodosta nähdään, että ympyrän keskipiste on
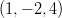 ja säde
ja säde  .
.
- Ellipsin akselit ovat koordinaattiakselien suuntaiset, ison akselin pituus on
 , ja pienen akselin pituus on
, ja pienen akselin pituus on  . Määritetään ellipsin
yhtälö.
. Määritetään ellipsin
yhtälö.
Ellipsin kaava on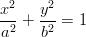 , missä
, missä  on puolet ison akselin
pituudesta ja
on puolet ison akselin
pituudesta ja 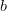 puolet pienen akselin pituudesta. Kysytyn ellipsin
yhtälö saadaan sijoittamalla arvot
puolet pienen akselin pituudesta. Kysytyn ellipsin
yhtälö saadaan sijoittamalla arvot 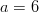 ja
ja 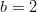 .
.

Yhtälö voidaan muuttaa toisen asteen käyrän muotoon kertomalla puolittain luvulla
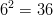 .
.
- Origokeskeisen R-säteisen pallon sekä ruuvipinnan parametriesitykset.
 Esimerkkejä pintojen parametriesityksistä
Esimerkkejä pintojen parametriesityksistä

Harjoitustehtäviä
- Mikä on ympyrän yhtälö, kun
- keskipiste on
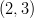 ja säde on
ja säde on 
- keskipiste on
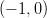 ja säde on
ja säde on 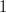
- keskipiste on
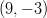 ja säde on
ja säde on  ?
?
- keskipiste on
- Onko piste
 ympyrän
ympyrän 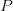 sisä- vai ulkopuolella?
sisä- vai ulkopuolella?
-
- Määritä pisteiden kautta kulkevan ympyrän yhtälö:
-
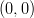 ,
,  ja
ja 
-
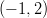 ,
, 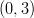 ja
ja 
-
- Määritä ympyrän tangentti, joka kulkee pisteen
 kautta
kautta
-
- Mikä 2. asteen käyrä?
-
Tehtävien vastaukset: