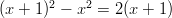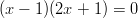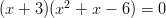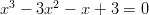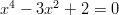Polynomiyhtälöt

Polynomiyhtälön p(x) = 0 ratkaisut — juuret — ovat polynomin p(x) nollakohdat. Ensimmäisen ja toisen asteen yhtälön ratkaisukaavat sisältyvät koulukurssiin. Kolmannen ja neljännen asteen yhtälöille on myös olemassa ratkaisukaavat, mutta nämä ovat varsin monimutkaisia. Viidennestä asteesta eteenpäin yleisiä juurilausekkeisiin perustuvia ratkaisukaavoja ei ole. Erikoistapauksiin soveltuvia menettelyjä on, mutta useimmiten tyydytään numeerisiin menetelmiin, joilla saadaan juurten likiarvot halutulla desimaalimäärällä.
 Ensimmäisen ja toisen asteen yhtälöt
Ensimmäisen ja toisen asteen yhtälöt Korkeampien asteiden yhtälöt
Korkeampien asteiden yhtälöt Algebran peruslause
Algebran peruslause

Esimerkkejä
- Ratkaistaan yhtälö
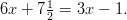
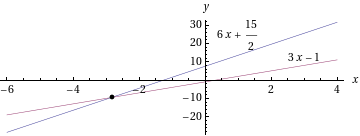
Vähennetään kummaltakin puolelta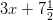 , jolloin vakiot ja
muuttujat saadaan eri puolille.
, jolloin vakiot ja
muuttujat saadaan eri puolille.
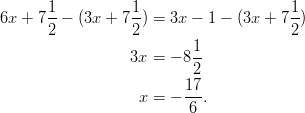
- Ratkaistaan 2. asteen yhtälö
 käyttämällä
ratkaisukaavaa.
käyttämällä
ratkaisukaavaa.
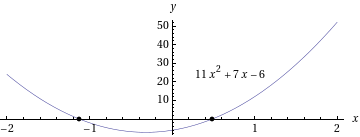

Yhtälöllä on kaksi eri ratkaisua:
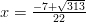 ja
ja 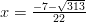 .
.
- Ratkaistaan 2. asteen yhtälö
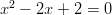 neliöksi täydentämällä.
neliöksi täydentämällä.
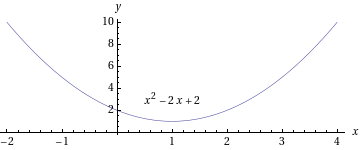
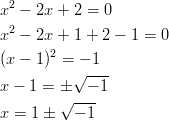
Neliöjuuressa on negatiivista, jolloin reaalisia ratkaisuja ei ole. Kompleksiset juuret saamme käyttämällä tietoa
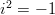 , josta
johdamme että
, josta
johdamme että  .
.
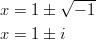
- Ratkaistaan 3. asteen yhtälö
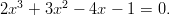
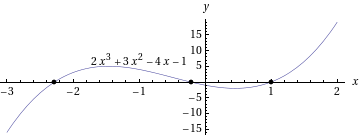
Arvataan eräs ratkaisu , jolla
, jolla  . Nyt voidaan
jakaa yhtälö termillä
. Nyt voidaan
jakaa yhtälö termillä  .
.
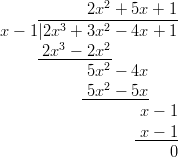
Yhtälö voidaan kirjoittaa muodossa
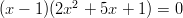 , ja
ratkaisemalla polynomin
, ja
ratkaisemalla polynomin 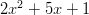 nollakohdat saamme yhtälön
loput ratkaisut:
nollakohdat saamme yhtälön
loput ratkaisut:
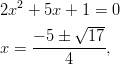
Yhtälö ratkeaa kun
 tai
tai 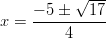 .
.
- Kolmannen asteen yhtälölle on myös olemassa yleinen ratkaisukaava,
mutta tavallisesti yhtälön ratkaiseminen muilla keinoilla on paljon
helpompaa.
3. asteen yhtälön ratkaisukaava
- Ratkaistaan bikvadraattinen yhtälö
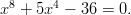

Tehdään sijoitus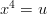 ja ratkaistaan saatu 2. asteen yhtälö.
ja ratkaistaan saatu 2. asteen yhtälö.

Suoritetaan takaisinsijoitus. Kaikkien kompleksisten juurten laskemisessa auttaa tieto
 .
.

Yhtälöllä on siis vain 2 reaalista juurta. Kompleksilukujen joukossa saadaan polynomiyhtälön kaikki juuret ratkaistua. Kompleksilukujen hallitseminen ei kuitenkaan kuulu tämän materiaalin aihepiiriin.

Harjoitustehtäviä
- Ratkaise yhtälöt:
-
- Ratkaise yhtälöt:
-
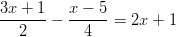
-
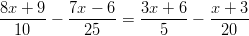
-
 (Ratkaise
(Ratkaise  muuttujien
muuttujien  ja
ja 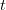 suhteen sekä
suhteen sekä
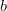 muuttujien
muuttujien  ja
ja  suhteen,
suhteen, 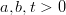 )
)
-
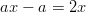 .
.
-
- Ratkaise yhtälöt:
-
- Ratkaise yhtälöt:
-
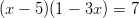
-
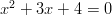
-

-

-
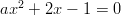 .
.
-
- Ratkaise yhtälöt:
-
- Ratkaise yhtälöt:
-
Tehtävien vastaukset: