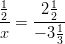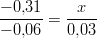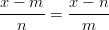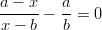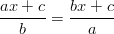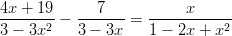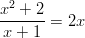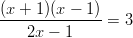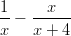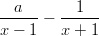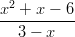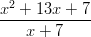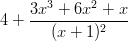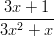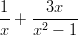Rationaalifunktiot

Lauseketta, jossa polynomi jaetaan polynomilla, kutsutaan rationaalifunktioksi. Tämä on määritelty kaikkialla muualla paitsi nimittäjän nollakohdissa. Rationaalifunktioita sievennetään erilaisiin muotoihin sen mukaan, mitä lausekkeella on tarkoitus tehdä tai millaisia ominaisuuksia halutaan tutkia. Osoittajapolynomin jakaminen nimittäjäpolynomilla, ts. osamäärän ja jakojäännöksen muodostaminen on yksi tapa sieventää lauseketta.
Rationaalifunktion kuvaajalla on asymptootteja. Nämä ovat yleensä suoria, joita kuvaaja rajatta lähestyy, kun xy-tasossa siirrytään jossakin suunnassa äärettömyyteen. Asymptoottina voi myös olla toisen tai korkeamman asteen polynomin kuvaaja (paraabeli, kuutioparaabeli jne.).

Esimerkkejä
- Ratkaistaan nollakohdat.
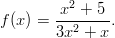
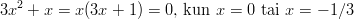
Yhtälö on määritelty koko
 :ssä paitsi pisteissä
:ssä paitsi pisteissä  ja
ja  . Rationaalifunktion nollakohdat määrittelyjoukossa
ovat samoja kuin osoittajan
. Rationaalifunktion nollakohdat määrittelyjoukossa
ovat samoja kuin osoittajan 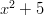 nollakohdat, joita ei reaalilukujen
joukossa ole. Rationaaliyhtälöllä ei
siis ole ratkaisuja. Rationaaliyhtälöllä on pystysuorat asymptootit
kohdissa
nollakohdat, joita ei reaalilukujen
joukossa ole. Rationaaliyhtälöllä ei
siis ole ratkaisuja. Rationaaliyhtälöllä on pystysuorat asymptootit
kohdissa  ,
, 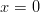 sekä
sekä 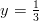 .
.
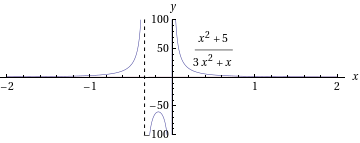
- Ratkaistaan rationaalifunktion nollakohdat.

Rationaalilauseke on määritelty kaikkialla paitsi pisteissä
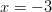 ja
ja
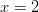 . (Tarkista!) Osoittajan nollakohdat ovat
. (Tarkista!) Osoittajan nollakohdat ovat 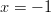 ja
ja  , eli
lausekkeen nollakohtia on vain yksi:
, eli
lausekkeen nollakohtia on vain yksi:  .
.
Tämä varmistuu, kun jakaa polynomit tekijöihinsä nollakohtiensa avulla: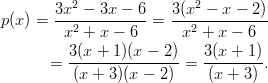

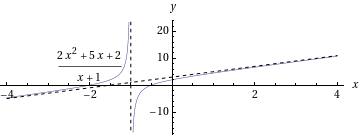
- Etsitään rationaalifunktion asymptootit.
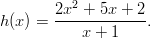
Koska osoittajan merkki on korkeampi kuin nimittäjän, voidaan suorittaa polynomien jakolasku.
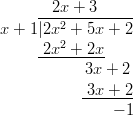

 :n asymptootteja ovat suorat
:n asymptootteja ovat suorat  sekä
sekä 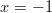 .
.

Harjoitustehtäviä
- Ratkaise yhtälöt:
-
- Ratkaise rationaaliyhtälöt:
-
- Etsi ratioonalifunktioiden nollakohdat:
-
- Määritä rationaalifunktioiden asymptootit:
-
Tähtävien vastaukset: