![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Rationaalifunktiot [ 1 2
]
Rationaalifunktiot [ 1 2
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) polynomit
polynomit
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Rationaalifunktiot [ 1 2
] Rationaalifunktiot [ 1 2
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) polynomit polynomit
KATSO MYÖS: |
|
Rationaalifunktion r(x) = p(x)/q(x) (missä p(x) ja q(x) polynomeja) asymptootti on suora tai käyrä, jota kuvaaja y = r(x) rajatta lähestyy, kun xy-tasossa jollakin tavoin siirrytään äärettömyyteen.
Nimittäjän q(x) nollakohdat ak antavat kuvaajan pystysuorat asymptootit x = ak.
Näissä kohdissa funktion r(x) raja-arvo on + tai -
tai - ; mahdollisesti eri puolilta
lähestyttäessä erilainen.
; mahdollisesti eri puolilta
lähestyttäessä erilainen.
Jos rationaalifunktio r(x) kirjoitetaan muotoon r(x) = u(x) + v(x)/q(x), missä polynomi v(x) on alempaa astetta kuin polynomi q(x), on
limx ±
± [r(x) - u(x)] = limx
[r(x) - u(x)] = limx ±
± v(x)/q(x) = 0.
v(x)/q(x) = 0.
Tällöin rationaalifunktion kuvaaja y = r(x) lähestyy käyrää y = u(x), kun
x  ±
± .
.
Jos polynomi u(x) on astetta 0, ts. u(x) = c0 = vakio, on rationaalifunktion kuvaajalla vaakasuora asymptootti y = c0.
Jos asteluku on 1, on u(x) = c1x + c0 ja rationaalifunktiolla on vino asymptootti y = c1x + c0.
Jos u(x) on korkeampaa astetta, sanotaan, että rationaalifunktiolla on käyräviivainen asymptootti y = u(x).
Esimerkki: Rationaalifunktiolla
r(x) = 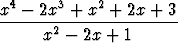 = x2 +
= x2 + 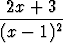
on pystysuora asymptootti x = 1 ja käyräviivainen asymptootti y = x2. Kuvaaja:
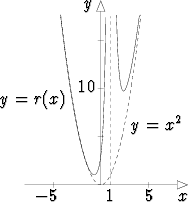
![[#]](kuvat/msam10-c-4.gif) funktio funktio![[#]](kuvat/msam10-c-4.gif) polynomi polynomi![[#]](kuvat/msam10-c-4.gif) käyrä (taso-) käyrä (taso-)![[#]](kuvat/msam10-c-4.gif) kuvaaja kuvaaja![[#]](kuvat/msam10-c-4.gif) nimittäjä nimittäjä![[#]](kuvat/msam10-c-4.gif) raja-arvo (funktion) raja-arvo (funktion)![[#]](kuvat/msam10-c-4.gif) asteluku asteluku |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12