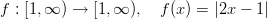Reaalifunktiot

Koulukurssi käsittelee lähes yksinomaan reaalifunktioita, so. reaalimuuttujan reaaliarvoisia funktioita. Tällaisia ovat esimerkiksi x2, |x + 1| ja 1∕x. Kaksi ensimmäistä on määritelty kaikilla reaaliarvoilla, viimeinen muualla paitsi origossa, so. arvolla x = 0. Alkeisfunktioita ovat tavalliset lausekkeiden rakennuspalikat, ts. lähes kaikki koulukurssin funktiot. Esimerkkinä reaalifunktiosta, jota yleensä ei lueta alkeisfunktioihin, on normaalijakauman kertymäfunktio

Tätä ei voida lausua yksinkertaisemmin alkeisfunktioiden avulla.
Reaalifunktioiden perusominaisuuksia ovat kasvavuus ja vähenevyys. Näiden määritelmät voivat pohjautua derivaatan käsitteeseen, mutta määritelmät voidaan asettaa myös yleisemmin, jolloin derivaattaa ei tarvita. Kasvavuudella saatetaan joskus tarkoittaa myös aitoa kasvavuutta, vastaavasti vähenevyydellä.
Perusominaisuuksia ovat myös jaksollisuus, parillisuus ja parittomuus.
 Funktion kasvavuus ja vähenevyys
Funktion kasvavuus ja vähenevyys Funktion jaksollisuus, parittomuus ja parillisuus
Funktion jaksollisuus, parittomuus ja parillisuus
Jos jokaista funktion f maalijoukon alkiota y vastaa yksikäsitteinen lähtöjoukon alkio x, funktiolla on käänteisfunktio. Ehdon voimassaoloa voidaan tutkia esimerkiksi ratkaisemalla yhtälö y = f(x) muuttujan x suhteen. Jos yhtälö ratkeaa yksikäsitteisesti y:stä riippumatta, käänteisfunktio on olemassa. Aidosti kasvavalla funktiolla on käänteisfunktio, mutta aito kasvavuus ei ole välttämätöntä käänteisfunktion olemassaololle (joskin ehkä tavallisin tapaus).

Esimerkkejä
- Parillisia funktioita ovat esimerkiksi
 ja
ja  .
Ne ovat symmetrisiä y-akselin suhteen.
.
Ne ovat symmetrisiä y-akselin suhteen. 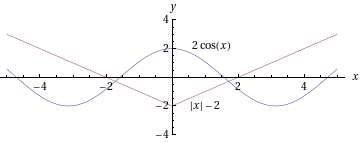
Parittomat funktiot ovat symmetrisiä origon suhteen, esimerkkinä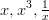 ja
ja 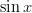 .
.
Funktioita, jotka eivät ole parittomia tai parillisia ovat esimerkiksi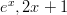 ja
ja  .
.
- Funktio
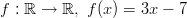 on kasvava.
on kasvava.

Kasvavuus nähdään kuvaajasta, mutta kuvaajasta katsominen ei useimmiten ole riittävä perustelu matematiikassa. Valitaan .
.
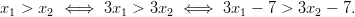
- Funktion
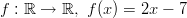 käänteiskuvaaja
on
käänteiskuvaaja
on 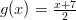 . Käänteiskuvaus on olemassa, koska funktio kuvaa
jokaisen luvun yksikäsitteisesti ja jokainen maalijoukon alkio tulee
kuvatuksi.
. Käänteiskuvaus on olemassa, koska funktio kuvaa
jokaisen luvun yksikäsitteisesti ja jokainen maalijoukon alkio tulee
kuvatuksi.

Funktion ja sen käänteiskuvauksen yhdistetty kuvaus on identiteettikuvaus.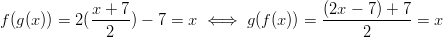

Harjoitustehtäviä
- Onko funktio
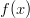 parillinen, pariton tai jaksollinen, kun
parillinen, pariton tai jaksollinen, kun
-
- Määritä funktion
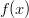 käänteisfunktio
käänteisfunktio  , jos sellainen on
olemassa, kun
, jos sellainen on
olemassa, kun
-
Tehtävien vastaukset:

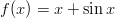
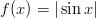

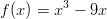
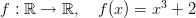
![f : ℝ → [− 1,1], f(x) = sin(x)](rfunktio21x.gif)