| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | LINEAARIALGEBRA |
Vektoriavaruuden kanta
Jos vektoriavaruuden (V, +, . ) joukon V äärellinen osajoukko {X 1,...,Xn} generoi vektoriavaruuden (V, +, . ), toisin sanoen jos

niin sanotaan, että (V, +, . ) on äärellisesti generoitu.
Määritelmä. Vektoriavaruuden (V, +, . ) (V  {
{ }) joukon V osajoukkoa B = {X
1,...,Xn}
sanotaan vektoriavaruuden kannaksi, jos
}) joukon V osajoukkoa B = {X
1,...,Xn}
sanotaan vektoriavaruuden kannaksi, jos
(i) B generoi vektoriavaruuden (V, +, . ),
(ii) B on lineaarisesti riippumaton.
Nolla-avaruuden { } kannaksi sovitaan tyhjä joukko.
} kannaksi sovitaan tyhjä joukko.
Lause. Joukko B = {X1,...,Xn} on vektoriavaruuden (V, +, . ) kanta jos ja vain jos jokainen
vektori X  V voidaan esittää yksikäsitteisesti vektorien X1,...,Xn lineaarikombinaationa eli
muodossa
V voidaan esittää yksikäsitteisesti vektorien X1,...,Xn lineaarikombinaationa eli
muodossa

Tätä esitystä sanotaan vektorin kantaesitykseksi. Alkioita a1,...,an sanotaan vektorin X koordinaateiksi kannan B suhteen.
Todistus. Olkoon B vektoriavaruuden (V, +, . ) kanta. Koska kanta generoi vektorijoukon V, voidaan jokainen joukon V vektori X lausua muodossa

Todistetaan vielä esityksen yksikäsitteisyys. Jos vektorilla X olisi toinen kantaesitys

niin vähentämällä toinen yhtälö ensimmäisestä saadaan
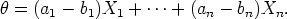
Koska kannan vektorit X1,...,Xn ovat lineaarisesti riippumattomia niin viimeiselle yhtälölle on olemassa vain triviaali ratkaisu ai - bi = 0 kaikilla i = 1,...,n. Siis ai = bi kaikilla i = 1,...,n. Täten kantaesitys on yksikäsitteinen.
Oletetaan kääntäen, että kaikilla vektorijoukon V vektoreilla on yksikäsitteinen esitys vektorien X1 , ... , Xn lineaarikombinaationa. Tämän perusteella V = L(X1,...,Xn). Toiseksi pitää todistaa vielä, että vektorit ovat lineaarisesti riippumattomia. Tarkastellaan lineaarista relaatiota

Tämä on nollavektorin esitys vektorien lineaarikombinaationa. Toisaalta myös
0 . X
1 +  + 0 . X
n =
+ 0 . X
n =  , joten esityksen yksikäsitteisyyden perusteella on ci = 0 kaikilla
i = 1, ... , n. Joukko {X1,...,Xn} on siis lineaarisesti riippumaton.
, joten esityksen yksikäsitteisyyden perusteella on ci = 0 kaikilla
i = 1, ... , n. Joukko {X1,...,Xn} on siis lineaarisesti riippumaton. ![[]](images/msam10-c-3.gif)