Aliavaruuden dimensio

Lause. Olkoon (V, +, ^. ) äärellisulotteinen vektoriavaruus. Olkoon (U, +, ^. ) vektoriavaruuden (V, +, ^. ) aliavaruus. Silloin

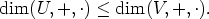
Jos (U, +, ^. ) on aito aliavaruus, on dim(U, +, ^. ) < dim(V, +, ^. ).

Todistus. Merkitään dim(V, +, ^. ) = n. Jokainen enemmän kuin n vektoria sisältävä joukon U osajoukko on lineaarisesti riippuva. Nimittäin tällaiset joukot ovat myös joukon V osajoukkoja ja sivun Vektoriavaruuden dimensio ensimmäisen lauseen mukaan ne ovat lineaarisesti riippuvia. Olkoon {X₁,...,X_m} U jokin lineaarisesti riippumaton joukko, jossa on suurin mahdollinen määrä vektoreita, siis m < n. Silloin L(X₁,...,X_m) = U, sillä muuten sivun Vektoriavaruuden dimensiosta lemman nojalla olisi joukossa U lineaarisesti riippumaton joukko, jossa olisi m + 1 vektoria. Joukko {X₁,...,X_m} on siis aliavaruuden (U, +, ^. ) kanta. Täten dim(U, +, ^. ) = m < n.

Jos m = n, niin saatu aliavaruuden (U, +, ^. ) kanta on myös vektoriavaruuden (V, +, ^. ) kanta, siis U = V. Tästä seuraa, että jos aliavaruus on aito, on m < n.

Huomaa, että sivun Vektoriavaruuden dimensiosta viimeisen lauseen mukaan aliavaruuden kanta voidaan aina täydentää koko avaruuden kannaksi.

Tutkitaan edellisen lauseen sovelluksena vektoriavaruuden (³, +, ^. ) aliavaruuksia. Jos (H, +, ^. ) on jokin aliavaruus, niin lauseen nojalla 0 < dim(H, +, ^. ) < 3.

Jos dim(H, +, ^. ) = 0, on H = {} siis nolla-avaruus.

Jos dim(H, +, ^. ) = 1, niin joukon H muodostavat jonkin vektorin kaikki skalaarimonikerrat. Toisin sanoen H sisältää kaikki pisteet, jotka ovat jollakin origon kautta kulkevalla suoralla.

Jos dim(H, +, ^. ) = 2, niin H sisältää kaikki joidenkin kahden lineaarisesti riippumattoman vektorin (u₁,v₁,w₁) ja (u₂,v₂,w₂) lineaarikombinaatiot. Tämä tarkoittaa sitä, että H sisältää kaikki sellaiset pisteet, jotka ovat jollain origon kautta kulkevalla tasolla.

Jos dim(H, +, ^. ) = 3, on H = ³.

Linkit:
Vektoriavaruuden dimensio
Vektoriavaruuden dimensiosta