Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		LINEAARIALGEBRA
 

Cramerin säännön todistus

Olkoon A = (A(1),...,A(n)) ja X = (x 1,x2,...,xn)T ja B = (b 1,b2,...,bn)T sekä

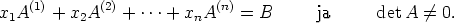
(1) (2) (n) x1A + x2A + ...+ xnA = B ja detA /= 0.

Muistetaan, että sivun Transponoidun matriisin determinantti huomautuksen perusteella ovat determinantin perusominaisuudet (D1)-(D6) voimassa vaikka niissä sana vaakarivi korvataan sanalla pystyrivi.

Kun korvataan i :s pystyrivi matriisin A determinantissa sarakkeella B, saadaan

det(A(1),...,B, ...,A(n)) = det(A(1),...,x1A(1) + x2A(2) + ...+ xnA(n),...,A(n)).

Käyttämällä determinantin summahajotelmaa (D2) yhtälön oikeaan puoleen saadaan se muotoon

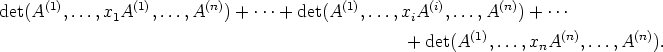det(A(1),...,x1A(1),...,A(n)) + ...+ det(A(1),...,xiA(i),...,A(n)) + ... (1) (n) (n) + det(A ,...,xnA ,...,A ).
Edelleen determinantin sarakkeen yhteisen tekijän siirron (D1) perusteella saadaan edellinen lauseke muotoon
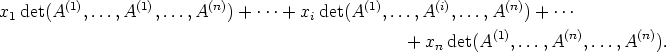(1) (1) (n) (1) (i) (n) x1det(A,...,A ,...,A ) + ...+ xi det(A ,...,A ,...,A ) + ... + x det(A(1),...,A(n),...,A(n)). n
Kaikissa paitsi i :nnessä tämän summalausekkeen termin determinantissa esiintyy sama sarake kahteen kertaan. Näiden determinanttien arvo on ominaisuuden (D5) perusteella nolla ja täten edellisen summan arvo on
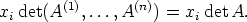
xidet(A(1),...,A(n)) = xidet A.

Siis

det(A(1),...,B, ...,A(n)) = xidet A.

Koska det A/=0, voidaan xi ratkaista edellisestä yhtälöstä ja saadaan väite.

Linkit:
Cramerin sääntö
Determinantin perusominaisuuksia
Transponoidun matriisin determinantti