Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		LINEAARIALGEBRA
 

Cramerin sääntö

Jos yhtälöryhmän

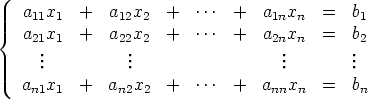
{ a11x1 + a12x2 + ... + a1nxn = b1 a21x1 + a22x2 + ... + a2nxn = b2 ... ... ... ... an1x1 + an2x2 + ... + annxn = bn

kertoimista muodostuva determinantti

||a a ... a || || 11 12 1n || det A = |a21 a22 ... a2n |/= 0, || ... ... ... || ||a a ... a || n1 n2 nn

niin yhtälöryhmällä on tarkalleen yksi ratkaisu, nimittäin

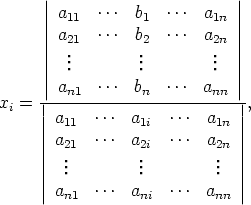
| | | a ... b ... a | || 11 1 1n || || a21 ... b2 ... a2n || | ... ... ... | || a ... b ... a || xi = |--n1-------n--------nn--|, || a11 ... a1i ... a1n || | a21 ... a2i ... a2n | || . . . || || .. .. .. || | an1 ... ani ... ann |

kun 1 < i < n. Ratkaisun osoittajassa on siis matriisin A determinantin i:s sarake korvattu yhtälöryhmän vakiotermisarakkeella.

Sama asia voidaan esittää lyhyemmin käyttämällä apuna matriisin pystyriviesitystä. Olkoon A = (A(1) , ... , A(n)) ja X = (x 1,x2,...,xn)T ja B = (b 1,b2,...,bn)T . Jos

x1A(1) + x2A(2) + ...+ xnA(n) = B

ja

detA /= 0,

niin yhtälöryhmällä on tarkalleen yksi ratkaisu, nimittäin

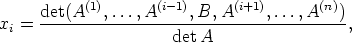
(1) (i- 1) (i+1) (n) x = det(A---,...,A----,B,-A-----,...,A---), i det A

kun i = 1, ... ,n.

Linkit:
Determinantti
Lineaariset yhtälöt ja yhtälöryhmät
Cramerin säännön todistus