Homogeeninen yhtälöryhmä

Lause. Jos lineaarisen homogeenisen yhtälöryhmän

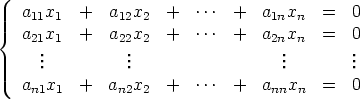
kertoimista muodostuvan matriisin A determinantti on nollasta eroava, on yhtälöryhmällä vain triviaali ratkaisu. Jos kyseinen determinantti on nolla, on yhtälöryhmällä myös muita ratkaisuja.

Todistus. Jos det A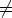0, niin yhtälöryhmällä on Cramerin säännön nojalla yksikäsitteinen ratkaisu. Koska yhtälöryhmällä on aina triviaali ratkaisu, ei sillä voi tässä tapauksessa olla muita ratkaisuja.

Oletetaan, että det A = 0. Voidaan olettaa, että kaikki matriisin alkiot eivät ole nollia (jos kaikki kertoimet olisivat nollia, olisi selvää, että yhtälöryhmällä on epätriviaaleja ratkaisuja). On siis olemassa sellainen luku k, 1 < k < n, että matriisilla A on ainakin yksi k-rivinen alideterminantti, joka on nollasta eroava, ja jokainen useampirivinen alideterminantti on nolla. Vaihtamalla tarvittaessa yhtälöryhmässä yhtälöiden ja tuntemattomien järjestystä saadaan

(1)

kaikilla r = 1, 2,...,n, sillä jos 1 < r < k, on determinantissa kaksi samaa vaakariviä, joten se on ominaisuuden (D5) mukaan nolla. Jos taas k + 1 < r < n, on determinantti (k + 1)-rivinen matriisin A alideterminantti ja siis oletuksen mukaan nolla. Kehitetään tämä determinantti alimman vaakarivin mukaan ja merkitään vastaavia komplementteja D₁,D₂,...D_k+1 (nämä eivät riipu luvusta r). Silloin kaikilla 1 < r < n saadaan

Täten tarkasteltavalla yhtälöryhmällä on ratkaisu

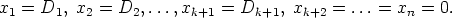
Saatu ratkaisu on epätriviaali, koska yhtälön (1) mukaan alideterminantti D_k+1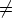0.

Linkit:
Lineaariset yhtälöt ja yhtälöryhmät
Cramerin sääntö
Determinantin perusominaisuuksia