Lagrangen lauseen sovellus lukuteoriaan

Palautetaan mieleen alkuluokkien modulo n joukko

Esimerkkejä ryhmästä, 2 -sivulla todetaan, että tämä joukko muodostaa ryhmän jäännösluokkien kertolaskun  ^.  = suhteen. Ryhmän neutraalialkio on .

Ryhmän (, ^. ) kertaluvulle on määritelty lukuteoriassa oma funktio.

Määritelmä. Eulerin -funktio, (n), on niiden kokonaislukujen m lukumäärä, joille syt(m,n) = 1 ja 1 < m < n.

Siis = (n). Jos n = p on alkuluku, niin (p) = p - 1. Esimerkkinä todetaan, että (10) = 4, sillä luvut 1, 3, 7, 9 ovat suhteellisia alkulukuja luvun 10 kanssa ja nämä ovat ainoita, jotka ovat positiivisia ja enintään 10.

Lagrangen lauseen avulla voidaan todistaa seuraava lukuteoreettisesti tärkeä Eulerin lause.

Lause. [Eulerin lause] Jos syt(a,n) = 1, niin

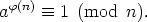
Todistus. Koska muodostaa ryhmän, jonka kertaluku on (n) niin Lagrangen lauseen toisen seurauslauseen mukaan kaikilla on = ⁽ⁿ⁾ = . Kirjoittamalla tämä kongruenssin muotoon saadaan väite.

Eulerin lauseen erikoistapauksena saadaan Fermat’n pikkulause.

Lause. [Fermat’n pikkulause] Olkoon p alkuluku. Jos p a, niin

Kaikille kokonaisluvuille on voimassa

Todistus. Jos p a eli syt(a,p) = 1, niin ensimmäinen väite seuraa Eulerin lauseesta, sillä (p) = p - 1. Toisen väitteen todistamiseksi huomataan ensin, että jos p a, niin a ^. a^p-1 a (mod p) eli a^p a (mod p). Jos p | a, niin a 0 (mod p), joten myös a^p 0 (mod p) eli a^p a (mod p).

Linkit:
Lagrangen lause
Esimerkkejä ryhmistä 2