smr235.html

Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003

RENGAS

Esimerkkejä alirenkaista

Esimerkki. Lukujoukot

V~ -- V~ -- Z[ n] = {a + b n |a,b (- Z} (n = - 1,± 2,± 3,...)

muodostavat kompleksilukujen renkaan (, +,^.) alirenkaita yhteenlaskun ja tulon suhteen. Nimittäin selvästi [ V~ --
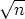n ] ja renkaan (, +,^.) ykkösalkio 1 = 1 + 0^. V~ --
n [ V~ --
n ]. Jos a_i + b_i V~
n [ V~ --
n ] (i = 1, 2), niin

V~ -- V~ -- V~ -- V~ -- (a1 + b1 n) - (a2 + b2 n) = a1- a2 + (b1 - b2) n (- Z[ n],

koska a₁ - a₂ ja b₁ - b₂ . Vastaavasti

V~ -- V~ -- V~ -- V~ -- V~ -V ~ -- (a1+b1 n) .(a2 + b2 n) = a1a2 + a1b2 n + a2b1 n + b1b2 n n V~ -- V~ -- = a1a2 + b1b2n + (a1b2 + a2b1) n (- Z[ n],

koska a₁a₂ + b₁b₂n

ja a₁b₂ + a₂b₁

. Alirengaskriteerin nojalla (

[

], +,^.) on alirengas.

Erikoistapauksessa n = -1 on kyseessä Gaussin kokonaisluvut.

Renkaita ([ V~ -
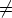
n ], +,^.) tarkasteltaessa oletetaan tavallisesti, että luku n on neliövapaa, toisin sanoen n ei ole jaollinen minkään ykköstä suuremman kokonaisluvun neliöllä. Silloin [ 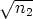V~ n1 ][ V~ n2 ] aina, kun n₁n₂.

Esimerkki. (POLYNOMIRENKAAT) Kaikkien reaalikertoimisten polynomien joukko

R[x] = {a0 + a1x + ...+ anxn |n > 0,ak (- R, k = 0,1,...,n}

on rengas polynomien yhteen- ja kertolaskun suhteen. Tämä nähdään osoittamalla, että ([x], +, ^. ) on funktiorenkaan (C(), +,^.) (katso sivu Esimerkkejä renkaista) alirengas.

Selvästi [x] C() ja funktiorenkaan ykkösalkio 1 [x]. Suoraan laskemalla nähdään, että myös alirengaskriteerin ehdot (ii) ja (iii) toteutuvat.

Muita polynomirenkaita ovat esimerkiksi ([x], +,^.) ja ([x], +,^.), joista ensimmäisen alkiot ovat kaikki kokonaislukukertoimiset polynomit ja toisen alkiot ovat kaikki rationaalilukukertoimiset polynomit.

Linkit:
Alirengas
Esimerkkejä renkaista