Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		RENGAS
 

Kokonaisalue

Määritelmä. Renkaan (R, +, . ) alkiota a sanotaan nollanjakajaksi (zero divisor), jos a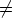/=0 R ja on olemassa sellainen b (- R, b/=0R, että

ab = 0R tai ba = 0R.

(Tällöin myös alkio b on nollanjakaja.)

Määritelmä. Rengasta (R, +, . ) sanotaan kokonaisalueeksi (integral domain), jos

     D1.   (R, +, . ) on kommutatiivinen ja
     D2.   renkaassa R ei ole nollanjakajia.

Kokonaisalueessa (D, +, . ) on voimassa supistamislaki: Olkoon a (- D ja a/=0 D. Silloin kaikilla b,c (- D,

jos ab = ac, niin b = c.

Nimittäin vasemmanpuoleinen yhtälö on ekvivalentti sen kanssa, että a(b-c) = 0D. Koska a ei ole nollanjakaja on oltava b - c = 0D.

Määritelmä. Kokonaisalueen (D, +, . ) karakteristika (characteristic)

{ pienin sellainen positiivinen kokonaisluku n, että n .1 = 0 , char(D)= D D 0, jos tä llaista lukua n ei ole olemasa.

Toisin sanoen char(D) on kokonaisalueen (D, +, . ) ykkösalkion 1 D kertaluku ryhmässä (D, +), paitsi jos kertaluku on ääretön, jolloin char(D) = 0.

Kokonaisalueen (D, +, . ) kaikilla nollasta eroavilla alkioilla a on sama kertaluku ryhmässä (D, +). Nimittäin yhtälö n . a = 0 D voidaan kirjoittaa muodossa (n . 1 D) . a = 0 D (katso sivu Renkaan aritmetiikkaa). Koska kokonaisalueessa D ei ole nollanjakajia, niin saatu yhtälö on yhtäpitävä yhtälön n . 1 D = 0D kanssa.

Lause. Kokonaisalueen (D, +, . ) karakteristika char(D) on joko 0 tai alkuluku.

Todistus. Oletetaan, että char(D) = n/=0. Kirjoitetaan luku n kahden luvun n1 ja n2 tulona n = n1n2, missä 0 < n1 < n ja 0 < n2 < n. Silloin 0D = n . 1 D = (n1 . n 2) . 1 D = (n1 . 1 D)(n2 . 1 D). Koska kokonaisalueessa D ei ole nollanjakajia, on ainakin toinen tulon tekijöistä 0D. Voidaan olettaa, että n1 . 1 D = 0D. Määritelmän mukaan n = char(D) on pienin luku, jolle n .   1 D = 0D. Täten n1 = n. Luvun n ainoa tekijöihinjako on siis n = n . 1, joten n on alkuluku. []

Linkit:
Renkaan aritmetiikkaa
Sykliset ryhmät