| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | KUNTA |
Esimerkkejä kunnista
Esimerkki. ( , +, . ), (
, +, . ), ( , +, . ) ja (
, +, . ) ja ( , +, . ) ovat (luku)kuntia. Kuten sivulla
Esimerkkejä renkaista todetaan, nämä kaikki ovat kommutatiivisia renkaita. Lisäksi
on helppo huomata, että kaikilla joukkojen
, +, . ) ovat (luku)kuntia. Kuten sivulla
Esimerkkejä renkaista todetaan, nämä kaikki ovat kommutatiivisia renkaita. Lisäksi
on helppo huomata, että kaikilla joukkojen  \{0},
\{0},  \{0} ja
\{0} ja  \{0} alkioilla on
käänteisalkiot.
\{0} alkioilla on
käänteisalkiot.
Kokonaislukujen muodostama rengas ( , +, . ) ei ole kunta, sillä vaikka se onkin
kommutatiivinen rengas, niin sen nollasta eroavilla alkioilla ei ole käänteisalkioita joukossa
, +, . ) ei ole kunta, sillä vaikka se onkin
kommutatiivinen rengas, niin sen nollasta eroavilla alkioilla ei ole käänteisalkioita joukossa
 \{0}. Kokonaislukurengas (
\{0}. Kokonaislukurengas ( , +, . ) on esimerkki äärettömästä kokonaisalueesta, joka ei ole
kunta.
, +, . ) on esimerkki äärettömästä kokonaisalueesta, joka ei ole
kunta.
Esimerkki. Kaikkien rationaalifunktioiden joukko
![R(x) = {p(x)--|p(x),q(x) (- R[x], q(x) ei ole nollapolynomi},
q(x)](images/smr2610x.gif)
muodostaa kunnan funktioiden pisteittäisen yhteen- ja kertolaskun suhteen. (Huomaa, että
( [x], +, . ) on kommutatiivinen rengas, mutta ei kunta.)
[x], +, . ) on kommutatiivinen rengas, mutta ei kunta.)
Koska kunnan ( (x), +, . ) ykkösalkio on vakiopolynomi 1 ja kaikki tämän monikerrat
k = k . 1 (k
(x), +, . ) ykkösalkio on vakiopolynomi 1 ja kaikki tämän monikerrat
k = k . 1 (k 
 ) ovat erisuuria, on char(
) ovat erisuuria, on char( (x)) = 0.
(x)) = 0.
Esimerkki. Sivun Kunta lauseesta ja sivun Esimerkkejä nollanjakajista ja kokonaisalueista
neljännestä esimerkistä seuraa, että jäännösluokkarengas ( m, +, . ) on kunta jos ja vain jos m
on alkuluku.
m, +, . ) on kunta jos ja vain jos m
on alkuluku.
Olkoon p alkuluku. Jäännösluokkarenkaan ( p, +, . ) karakteristika on p, sillä p .
p, +, . ) karakteristika on p, sillä p .  =
=  =
= 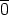 ja
kaikille kokonaisluvuille n, joille 0 < n < p, on n .
ja
kaikille kokonaisluvuille n, joille 0 < n < p, on n . 

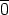 .
.
Koska 5 on alkuluku on ( 5, +, . ) kunta. Esitetään tämän kunnan yhteenlasku- ja
kertotaulut.
5, +, . ) kunta. Esitetään tämän kunnan yhteenlasku- ja
kertotaulut.

 5, +, . ) summa
5, +, . ) summa  +
+  .
.
Käyttämällä yllä olevaa kertotaulua nähdään, että  =
=  .
. 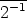 =
= 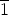 .
. 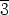 =
=  . Vastaavasti
. Vastaavasti
 =
=  .
. 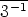 =
=  .
.  =
=  . Yhteenlaskutaulua käyttämällä saadaan, että
. Yhteenlaskutaulua käyttämällä saadaan, että
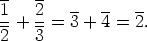
Linkit:
Esimerkkejä renkaista
Kunta