Kunta

Seuraavaksi esitetään kunnan määritelmä. Kunnan mallina on rationaalilukujen joukko, jossa on määritelty neljä peruslaskutoimitusta.

Määritelmä. Kolmikkoa (K, +, ^. ) sanotaan kunnaksi (field), jos

     K1.   (K, +, ^. ) on kommutatiivinen rengas (ei nollarengas) ja
     K2.   jokaisella joukon K nolla-alkiosta 0_K eroavalla alkiolla on käänteisalkio joukossa K, toisin sanoen renkaan K yksikköryhmä K^* = K \{0 _K}.

Kolmikko (K, +, ^. ) on siis määritelmän mukaan kunta jos ja vain jos se täyttää ehdot:

     K1’.   (K, +) on Abelin ryhmä (kunnan additiivinen ryhmä),
     K2’.   (K \{0_K}, ^. ) on Abelin ryhmä (kunnan multiplikatiivinen ryhmä),
     K3’.   a(b + c) = ab + ac ja (a + b)c = ac + bc kaikilla a,b,c K.

Jos ei vaadita kertolaskun kommutatiivisuutta, saadaan niin sanottu vinokunta (skew field) eli jakorengas (division ring).

Lause.

     (i)   Jokainen kunta on kokonaisalue.
     (ii)   Jokainen äärellinen kokonaisalue on kunta.

Todistus. (i) Olkoon (K, +, ^. ) kunta. Kunnan määritelmän nojalla (K, +, ^. ) on kommutatiivinen rengas, joten kokonaisalueen ehto D1. toteutuu. Osoitetaan vielä, ettei kunnassa ole nollanjakajia. Oletetaan, että ab = 0_K, joillakin a,b K, missä a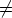0_K. Alkiolla a on käänteisalkio a^-1 kunnassa K, täten b = a^-1 . 0 _K = 0_K, mikä todistaa väitteen.

(ii) Olkoon (D, +, ^. ) äärellinen kokonaisalue. Nyt pitää osoittaa, että jokaisella kokonaisalueen D nolla-alkiosta eroavalla alkiolla on käänteisalkio joukossa D. Olkoon a D \{0_D}. Muodostetaan joukon D osajoukko D₀ = {ax | x D}. Soveltamalla supistamislakia kokonaisalueessa D nähdään, että ax₁ax₂ aina, kun x₁x₂. Koska D on äärellinen, tästä seuraa, että joukossa D₀ on yhtä monta alkiota kuin kokonaisalueessa D, siis D₀ = D. Silloin erityisesti kokonaisalueen D ykkösalkio 1_D on joukossa D₀, toisin sanoen on olemassa sellainen u D, että au = 1_D. Koska D on kommutatiivinen tämä tarkoittaa, että u = a^-1.

Linkit:
Rengas
Ryhmä
Kokonaisalue
Huomioita kunnasta