| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | KUNTA |
Huomioita kunnasta
Koska kunta on rengas, on siinä määritelty yhteen-, vähennys- ja kertolasku. Jos (K, +, . ) on
kunta ja a,b  K, niin vähennyslasku on a - b = a + (-b). Jakolasku määritellään tavalliseen
tapaan, kun b
K, niin vähennyslasku on a - b = a + (-b). Jakolasku määritellään tavalliseen
tapaan, kun b 0K :
0K :
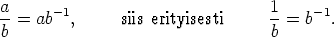
Kaikille a,b,c,d  K, kun b
K, kun b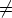 0K ja d
0K ja d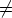 0K, saadaan soveltamalla renkaan laskulakeja,
että
0K, saadaan soveltamalla renkaan laskulakeja,
että
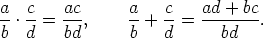
Osamäärillä  lasketaan siis samoin kuin murtoluvuilla. Huomaa myös, että
lasketaan siis samoin kuin murtoluvuilla. Huomaa myös, että  = a.
= a.
Jos ei ole sekaannuksen vaaraa, kunnassa (K, +, . ) merkitään usein

Koska kunta on kokonaisalue, sille on määritelty karakteristika char(K), ja tämä on joko 0 tai alkuluku sivun Kokonaisalue lauseen mukaan. Jos char(K) = 0, niin (K, +, . ) on ääretön kunta. Äärellisen kunnan karakteristika on alkuluku.
Jos char(K) = p on alkuluku, niin edellisessä yhtälössä n . 1 K = n on n = 0 jos ja vain jos p | n.
Koska kunta on rengas, voidaan puhua sen ihanteista. Seuraava lause käsittelee tämän asian tyhjentävästi.
Lause. Kunnan (K, +, . ) ainoat ihanteet ovat K ja {0 K}.
Todistus. Kuten sivulla Ihanne todetaan ovat K ja {0K} kunnan K ihanteita. Olkoon I kunnan
K ihanne ja I {0K}. Koska ihanteen alkiot ovat kunnan alkioita, niin kaikilla a
{0K}. Koska ihanteen alkiot ovat kunnan alkioita, niin kaikilla a  I on
olemassa käänteisalkio, joten ne ovat yksiköitä. Sivun Ihanne huomion mukaan tästä seuraa,
että I = K.
I on
olemassa käänteisalkio, joten ne ovat yksiköitä. Sivun Ihanne huomion mukaan tästä seuraa,
että I = K. ![[]](images/msam10-c-3.gif)
Olkoot (K, +, . ) ja (K', +', . ') kuntia. Rengashomomorfismia f : (K, +, . )  (K', +', . ')
sanotaan myös kuntahomomorfismiksi, vastaavaa rengasisomorfismia sanotaan
kuntaisomorfismiksi.
(K', +', . ')
sanotaan myös kuntahomomorfismiksi, vastaavaa rengasisomorfismia sanotaan
kuntaisomorfismiksi.
Lause. Jokainen kuntahomomorfismi f : (K, +, . )  (K', +', . ') on injektio ja siis indusoi
kuntaisomorfismin F : (K, +, . )
(K', +', . ') on injektio ja siis indusoi
kuntaisomorfismin F : (K, +, . )  (Im (f), +', . ').
(Im (f), +', . ').
Todistus. Sivun Rengashomomorfismin ydin ja kuva lauseen mukaan rengashomomorfismin ja
siis tässä tapauksessa kuntahomomorfismin ydin on ihanne. Edellisen lauseen mukaan siis ydin
on joko kunta itse tai nollaihanne. Jos ydin on K, niin silloin kaikilla a  K on f(a) = 0K.
Tämä on kuitenkin mahdotonta rengashomomorfismin postulaatin RH3 nojalla. Siis
kuntahomomorfismin ydin on {0K} ja täten sivun Rengashomomorfismin ydin ja kuva huomion
mukaan kuntahomomorfismi on injektio.
K on f(a) = 0K.
Tämä on kuitenkin mahdotonta rengashomomorfismin postulaatin RH3 nojalla. Siis
kuntahomomorfismin ydin on {0K} ja täten sivun Rengashomomorfismin ydin ja kuva huomion
mukaan kuntahomomorfismi on injektio.
Koska f : (K, +, . )  (K', +', . ') antaa surjektion f : (K, +, . )
(K', +', . ') antaa surjektion f : (K, +, . )  (Im (f), +', . '),
saadaan lauseen loppuosan väite.
(Im (f), +', . '),
saadaan lauseen loppuosan väite. ![[]](images/msam10-c-3.gif)
Edellisen lauseen mukaan kunnan (K, +, . ) kaikki homomorfiset kuvat ovat isomorfisia tämän kunnan kanssa.
Linkit:
Kunta
Kokonaisalue
Ihanne
Renkaan yksikköryhmä
Rengashomomorfismin ydin ja kuva
Renkaiden homomorfialause