| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | RENGAS |
Renkaiden homomorfialause
Lause. [Renkaiden homomorfialause] Jos f : (R, +, . )  (R', +', . ') on rengashomomorfismi,
niin
(R', +', . ') on rengashomomorfismi,
niin

Tarkemmin: f indusoi rengasisomorfismin

missä F(a + ker(f)) = f(a) kaikilla a  R.
R.
Todistus. Ryhmien homomorfialauseen nojalla kuvaus F : (R/ ker(f), +)  (Im (f), +') on
ryhmäisomorfismi. On siis todistettava, että kuvaus F toteuttaa homomorfiaehdot RH2 ja
RH3.
(Im (f), +') on
ryhmäisomorfismi. On siis todistettava, että kuvaus F toteuttaa homomorfiaehdot RH2 ja
RH3.
Kaikilla a,b 
 on
on

joten RH2 toteutuu. Lisäksi F(1R + ker(f)) = f(1R) = 1R' = 1Im (f), joten RH3 toteutuu. ![[]](images/msam10-c-3.gif)
Kuten ryhmillä, saadaan renkailla homomorfialauseen nojalla alla oleva kommutoiva diagrammi.
Olkoon I renkaan (R, +, . ) ihanne, silloin kuvausta 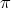

sanotaan (kanoniseksi) projektioksi. Kuvaus 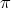 on rengashomomorfismi, sillä kaikilla a,b
on rengashomomorfismi, sillä kaikilla a,b  R
on
R
on
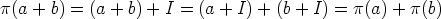
ja

Lisäksi 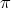 (1R ) = 1R + I = 1R/I. Kuvaus
(1R ) = 1R + I = 1R/I. Kuvaus 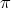 on triviaalisti surjektiivinen.
on triviaalisti surjektiivinen.
Olkoon f : (R, +, . )  (R', +', . ') rengashomomorfismi. Valitaan nyt I = ker(f).
Homomorfialauseen nojalla f(a) = F(a + ker(f)) = F(a + I) = F(
(R', +', . ') rengashomomorfismi. Valitaan nyt I = ker(f).
Homomorfialauseen nojalla f(a) = F(a + ker(f)) = F(a + I) = F(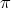 (a)) = (Fo
(a)) = (Fo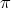 )(a) kaikilla
a
)(a) kaikilla
a  R, missä F on kuvaus (R/ ker(f), +, . )
R, missä F on kuvaus (R/ ker(f), +, . )  (Im (f), +', . '). Siis f = Fo
(Im (f), +', . '). Siis f = Fo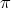 . Renkaan
(R, +, . ) homomorfiset kuvat vastaavat siis bijektiivisesti renkaan R jäännösluokkarenkaita.
. Renkaan
(R, +, . ) homomorfiset kuvat vastaavat siis bijektiivisesti renkaan R jäännösluokkarenkaita.

Linkit:
Ryhmien homomorfialause
Renkaiden homomorfia
Rengashomomorfismin ydin ja kuva