Renkaiden homomorfia

Määritelmä. Olkoot (R, +, ^. ) ja (R', +', ^. ') renkaita. Kuvausta f : (R, +, ^. ) (R', +', ^. ') sanotaan (rengas)homomorfismiksi, jos se täyttää ehdot:

     RH1.   f(a + b) = f(a) + 'f(b) a,b R,
     RH2.   f(a ^. b) = f(a) ^. 'f(b) a,b R,
     RH3.   f(1_R) = 1_R'.

Määritelmän mukaan kuvaus f : (R, +, ^. ) (R', +', ^. ') on rengashomomorfismi jos ja vain jos f on ryhmähomomorfismi (R, +) (R', +') ja sillä on ominaisuudet RH2 ja RH3. Ryhmähomorfismin ominaisuuksien perusteella rengashomomorfismi f : (R, +, ^. ) (R', +', ^. ') toteuttaa kaikilla a R ehdot

Lisäksi ehtojen RH2 ja RH3 nojalla

sillä f(a) ^. 'f(a^-1) = f(a ^. a^-1) = f(1 _R) = 1_R' ja samoin nähdään, että f(a^-1) ^. 'f(a) = 1 _R'.

Lause. Olkoon f : (R, +, ^. ) (R', +', ^. ') rengashomomorfismi.

     (i)   Jos (S, +, ^. ) on renkaan (R, +, ^. ) alirengas, niin (f(S), +', ^. ') on renkaan (R', +', ^. ') alirengas.
     (ii)  Jos I on renkaan (R, +, ^. ) ihanne, niin f(I) on renkaan (f(R), +', ^. ') ihanne.

Todistus. (i) Todistetaan väite käyttäen alirengaskriteeriä. Koska S on renkaan R alirengas, niin 1_R S. Lisäksi f(1_R) = 1_R', joten 1_R' f(S). Jos a',b' f(S), niin on olemassa sellaiset a, b S, että a' = f(a) ja b' = f(b). Nyt

koska a - b S alirengaskriteerin nojalla. Vastaavasti

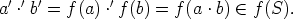
(ii) Kohdan (i) nojalla (f(R), +', ^. ') on rengas. Todistetaan väite käyttäen ihannekriteeriä. Koska I on ihanteena epätyhjä, samoin on f(I). Vastaavasti kuin kohdassa (i) todetaan, että kaikkien joukon f(I) alkioiden erotus kuuluu joukkoon f(I). Jos a' f(I), niin on olemassa sellainen a I, että a' = f(a). Vastaavasti kaikilla r' f(R) on olemassa sellainen r R, että r' = f(r). Nyt

koska ra I. Samoin nähdään, että a' ^. 'r' f(I) kaikilla a' f(I) ja r' f(R).

Linkit:
Ryhmien homomorfia
Alirengas
Ihanne