Alikunta

Määritelmä. Olkoon (K, +, ^. ) kunta ja F K. Kolmikko (F, +, ^. ) on kunnan K alikunta, jos (F, +, ^. ) on kunta.

Jos (F, +, ^. ) on kunnan (K, +, ^. ) alikunta, niin (F, +) on ryhmän (K, +) aliryhmä ja (F \{0_F }, ^. ) on ryhmän (K \{0 _R}, ^. ) aliryhmä. Tästä seuraa, että kuntien K ja F nolla-alkiot ja ykkösalkiot ovat samat.

Lause. (Alikuntakriteeri) Olkoon (K, +, ^. ) kunta ja F K. Kolmikko (F, +, ^. ) on kunnan K alikunta jos ja vain jos seuraavat ehdot toteutuvat:

     AK1.   Joukossa F on vähintään kaksi alkiota,
     AK2.   a - b F kaikilla a,b F,
     AK3.    F kaikilla a,b F, b0_K.

Todistus. Oletetaan ensin, että (F, +, ^. ) on kunnan (K, +, ^. ) alikunta. Kuten ennen lausetta todettiin on (F, +) on ryhmän (K, +) aliryhmä. Täten 0_K F ja aliryhmäkriteerin perusteella kaikilla a,b F on a - b F. Vastaavasti (F \{0_F }, ^. ) on ryhmän (K \{0 _R}, ^. ) aliryhmä, joten 1_K F ja ab^-1 = F.

Oletetaan kääntäen, että ehdot AK1-AK3 ovat voimassa. Ehtojen AK1 ja AK2 nojalla (F, +) on ryhmän (K, +) aliryhmä. Vastaavasti ehtojen AK1 ja AK3 nojalla (F \{0_F }, ^. ) on ryhmän (K \{0_K}, ^. ) aliryhmä. Koska lisäksi joukon F alkiot kunnan K alkioina toteuttavat distributiivilait, pitää väite paikkansa sivun Kunta toteamuksen perusteella.

Lause. Olkoon (K, +, ^. ) kunta ja I jokin indeksijoukko. Jos (K _i, +, ^. ) on kunnan K alikunta kaikilla i I, niin

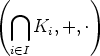
on kunnan K alikunta.

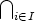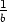
Todistus. Kaikkiin kunnan K alikuntiin sisältyvät alkiot 1_K ja 0_K, täten ne sisältyvät alikuntien leikkaukseen. Jos a,b K_i, niin a,b K_i kaikilla i I. Täten a - b K_i ja K_i kaikilla i I. Siis a - b K_i ja K_i. Väite seuraa alikuntakriteeristä.

Linkit:
Kunta
Aliryhmä