| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | KUNTA |
Esimerkkejä alikunnista
Esimerkki. Olkoon n (n 0, 1) neliövapaa kokonaisluku (toisin sanoen luvulla n
ei ole tekijänä mitään kokonaisluvun neliötä m2, missä m > 1). Osoitetaan, että
joukko
0, 1) neliövapaa kokonaisluku (toisin sanoen luvulla n
ei ole tekijänä mitään kokonaisluvun neliötä m2, missä m > 1). Osoitetaan, että
joukko

muodostaa kunnan ( , +, . ) alikunnan. Jos n > 0, on tämä alikunta myös kunnan (
, +, . ) alikunnan. Jos n > 0, on tämä alikunta myös kunnan ( , +, . )
alikunta.
, +, . )
alikunta.
Koska 

 (
( ), toteutuu alikuntakriteerin ehto AK1.
), toteutuu alikuntakriteerin ehto AK1.
Oletetaan, että a + b , a' + b'
, a' + b'

 (
( ). Silloin
). Silloin
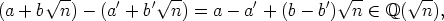
koska a - a'
 ja b - b'
ja b - b'
 . Täten ehto AK2 toteutuu.
. Täten ehto AK2 toteutuu.
Oletetaan lisäksi, että a' + b'
 0. Nyt
0. Nyt

Saatu tulos kuuluu kuntaan  (
(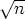 ), mikäli (a')2
- (b')2n
), mikäli (a')2
- (b')2n 0. Pitää siis osoittaa, että
a'- b'
0. Pitää siis osoittaa, että
a'- b'
 0. Jos a'- b'
0. Jos a'- b' = 0, niin a' = b'
= 0, niin a' = b' . Jos b' = 0, niin myös a' = 0, mistä
seuraisi, että a' + b'
. Jos b' = 0, niin myös a' = 0, mistä
seuraisi, että a' + b' = 0, mikä on ristiriita. Täten b'
= 0, mikä on ristiriita. Täten b' 0 (samoin myös a'
0 (samoin myös a' 0). Nyt
n =
0). Nyt
n = 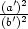 . Koska n
. Koska n 
 (n
(n 0, 1), niin myös (
0, 1), niin myös ( )2
)2 
 ja siis
ja siis 

 . Tästä seuraa, että
n on neliö, mikä on ristiriita. Siis a'- b'
. Tästä seuraa, että
n on neliö, mikä on ristiriita. Siis a'- b'
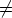 0 ja näin ollen ehto AK3 toteutuu.
0 ja näin ollen ehto AK3 toteutuu.
Esimerkki. Olkoon (K, +, . ) kunta ja char(K) = 2. Näytetään, että joukko {0 K, 1K} muodostaa kunnan K alikunnan. Koska joukossa {0K, 1K} on kaksi alkiota ehto AK1 toteutuu.
Koska char (K) = 2, on 1K + 1K = 0K ja tästä seuraa, että -1K = 0K - 1K = 1K.
Vastaavasti voidaan laskea muut erotukset ja nähdään, että ehto AK2 toteutuu. Ehto AK3
toteutuu, koska  = a molemmilla a
= a molemmilla a  {0K, 1K}. Väite seuraa alikuntakriteeristä.
{0K, 1K}. Väite seuraa alikuntakriteeristä.
Esimerkki. Olkoon (K, +, . ) kunta ja kuvaus f : (K, +, . )  (K, +, . ) homomorfismi
kunnalta itselleen. Merkitään
(K, +, . ) homomorfismi
kunnalta itselleen. Merkitään

Näytetään, että (F, +, . ) on kunnan (K, +, . ) alikunta. Kuntaa (F, +, . ) sanotaan homomorfismin f kiintokunnaksi.
Koska kuntahomomorfismi (katso sivu Renkaiden homomorfia) kuvaa aina f(1K) = 1K ja
f(0K ) = 0K , niin {0K, 1K} F. Täten alikuntakriteerin ehto AK1 toteutuu. Oletetaan, että
a, b
F. Täten alikuntakriteerin ehto AK1 toteutuu. Oletetaan, että
a, b  F. Silloin joukon F ja homomorfian määritelmän perusteella (katso sivu Renkaiden
homomorfia)
F. Silloin joukon F ja homomorfian määritelmän perusteella (katso sivu Renkaiden
homomorfia)

Täten a - b  F. Jos lisäksi b
F. Jos lisäksi b 0K, niin
0K, niin
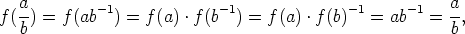
ja siis 
 F. Ehdot AK2 ja AK3 toteutuvat. Väite seuraa alikuntakriteeristä.
F. Ehdot AK2 ja AK3 toteutuvat. Väite seuraa alikuntakriteeristä.
Linkit:
Alikunta
Renkaiden homomorfia