| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | POLYNOMIRENKAAT |
Esimerkkejä kuntalaajennuksista polynomirenkaissa
Esimerkki. Tutkitaan reaalilukujen kuntaa ( , +, . ). Olkoon p(x) = x2 + 1. Kuten sivulla
Esimerkkejä polynomirenkaista todettiin on p(x) jaoton yli kunnan
, +, . ). Olkoon p(x) = x2 + 1. Kuten sivulla
Esimerkkejä polynomirenkaista todettiin on p(x) jaoton yli kunnan  . Merkitään
I =< x2 + 1 > . Sivun Polynomirenkaan jäännösluokkarenkaasta perusteella saadaan siis
kunta
. Merkitään
I =< x2 + 1 > . Sivun Polynomirenkaan jäännösluokkarenkaasta perusteella saadaan siis
kunta
![R[x]/I = {a + bx + I |a,b (- R},](images/smr2890x.gif)
jonka operaatiot ovat, kun a + bx + I,a' + b'x + I 
 [x]/I,
[x]/I,

 [x]/I.
[x]/I.
Saatu kunta on kompleksilukujen kunta ( , +, . ). Yhteyden näkee helpoiten, kun merkitään
a + bx + I = a + bi.
, +, . ). Yhteyden näkee helpoiten, kun merkitään
a + bx + I = a + bi.
Sivun Kuntalaajennus polynomirenkaassa lauseen todistuksen perusteella polynomin y2 + 1
nollakohta kunnassa ( [x]/I, +, . ) on x + I, siis 0 + 1 . i = i, kuten pitääkin.
[x]/I, +, . ) on x + I, siis 0 + 1 . i = i, kuten pitääkin.
Esimerkki. Polynomi p(x) = x2 + x +  on jaoton yli kunnan (
on jaoton yli kunnan ( 2, +, . ), sillä p(
2, +, . ), sillä p( ) =
) =  ja
p(
ja
p( ) =
) = 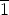 . Täten saadaan kunta, kun merkitään I =< p(x) >,
. Täten saadaan kunta, kun merkitään I =< p(x) >,
![Z2[x]/I = {a +-bx + I |a,b- (- Z2}
= {I,1 + I,x + I,1 + x + I}.](images/smr2897x.gif)
Kyseessä on siis neljän alkion kunta. (Tämä on Galois’n kunta GF(22).) Jos kunnan
alkioita merkitään seuraavasti: 0 = I (nolla-alkio), 1 = 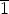 + I (ykkösalkio),
+ I (ykkösalkio), 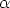 = x + I
ja
= x + I
ja  =
= 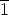 + x + I, saadaan additiiviselle ja multiplikatiiviselle ryhmälle seuraavat
taulut.
+ x + I, saadaan additiiviselle ja multiplikatiiviselle ryhmälle seuraavat
taulut.

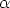
 laskettiin seuraavasti:
laskettiin seuraavasti:

Tauluja apuna käyttäen todetaan, että 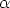 on polynomin x2 + x +
on polynomin x2 + x +  nollakohta. Nimittäin
nollakohta. Nimittäin

Linkit:
Esimerkkejä polynomirenkaista
Polynomirenkaan jäännösluokkarenkaasta
Kuntalaajennus polynomirenkaassa