Lineaarinen riippumattomuus

Funktioiden lineaarinen riippumattomuus on käsite, joka tulee käyttöön mm. lineaaristen differentiaaliyhtälöiden teoriassa. Tämä määritellään seuraavasti:

Määritelmä. Funktiot y₁(x),  y₂(x),  . . . ,  y_n(x) ovat lineaarisesti riippumattomia, jos yhtälö

_ky_k(x) = 0  eli  ₁y₁(x) + ₂y₂(x) + . . . + _ny_n(x) = 0

on voimassa kaikilla (tarkasteluväliin kuuluvilla) muuttujan x arvoilla ainoastaan siinä tapauksessa, että ₁ = ₂ = . . . = _n = 0.

Jos yhtälö toteutuu kaikilla muuttujan x arvoilla siten, että yksikin luvuista _k on 0, funktiot ovat lineaarisesti riippuvia.

Jos erityisesti jokin funktioista y_k(x) on nollafunktio, ts. = 0 kaikilla x, voidaan tätä vastaava kerroin _k valita nollasta eroavaksi, ja funktiot ovat siis lineaarisesti riippuvia.

Yhtälöä ₁ y₁ (x) + ₂y₂(x) + . . . + _ny_n(x) = 0 on ajateltava testiyhtälönä, joka on voimassa kaikilla muuttujan x arvoilla ja josta pyritään ratkaisemaan luvut _k. Ratkaisuksi kelpaa aina, että kaikki luvut _k ovat = 0, mutta tämä ei ratkaise lineaarista riippuvuutta tai riippumattomuutta. Oleellista on, löytyykö muita ratkaisuja. Jos ei, niin funktiot ovat lineaarisesti riippumattomat. Jos löytyy, niin ne ovat lineaarisesti riippuvat.

Jos funktiot ovat lineaarisesti riippuvia, on ainakin yksi kerroin 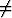0; olkoon esimerkiksi _p 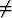0. Tällöin testiyhtälöstä voidaan ratkaista funktio y_p(x):

y_p(x) = - y_k(x).

Kahden funktion tapauksessa tämä merkitsee, että toinen on sama kuin toinen vakiolla kerrottuna: Jos ₁y₁ + ₂y₂(x) = 0 kaikilla x ja ₁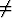0, niin

y₁(x) = y₂(x),   missä  = -.