![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Matematiikka tieteenä
Matematiikka tieteenä  Matematiikan
merkinnät [ 1 2 ]
Matematiikan
merkinnät [ 1 2 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Matematiikka tieteenä Matematiikka tieteenä  Matematiikan
merkinnät [ 1 2 ] Matematiikan
merkinnät [ 1 2 ]
ESITIEDOT: KATSO MYÖS: |
|
Nykyään käytössä olevat matematiikan merkinnät ovat kehittyneet vuosisatojen kuluessa eivätkä monet niistä ole kovinkaan vanhoja. Varsin tavallista on, että jonkin osa-alueen alkuperäisten ideoiden luoja ei lainkaan tuntisi niitä merkintöjä, joita käyttäen hänen nimeään kantavat tulokset nykyään esitetään.
Esimerkiksi antiikin Kreikan geometriassa tarkasteltiin janojen pituuksien keskinäisiä suhteita, mutta ei ilmaistu näitä algebrallisin lausekkein kuten nykyään. Algebra levisikin arabimaista Eurooppaan vasta keskiajan lopulla. Vielä 1500-luvun algebralliset merkinnät — mm. potenssien merkintä — poikkesivat nykyisestä.
Isaac Newtonin tapa esittää differentiaali- ja integraalilaskenta 1600-luvun lopulla
ei aivan helposti avaudu nykyajan lukijalle erilaisten merkintöjen ja osin
käsitteidenkin takia; alan perustavat merkintätavat ovat peräisin sen toiselta
kehittäjältä, Gottfried Wilhelm Leibnizilta. Suurimman osan differentiaali- ja
integraalilaskennan merkinnöistä on kuitenkin vakiinnuttanut 1700-luvulla
Leonhard Euler. Hän on myös ottanut käyttöön symbolit  , e ja i matematiikan
tärkeille vakioille.
, e ja i matematiikan
tärkeille vakioille.
Varsinkin painetussa tekstissä noudatetaan nykyään matematiikan merkinnöissä tapoja, joiden tarkoituksena on jäsentää lausekkeet mahdollisimman selvästi ja jo merkintätavalla osoittaa, minkä tyyppinen olio milloinkin on kyseessä.
Esimerkiksi erilaiset muuttujat, vakiot ja tarkemmin määräämättömät
funktiot kirjoitetaan kursivoituina: x = (-b ± 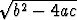 )/(2a), f(x).
Standardifunktioiden nimet sen sijaan kirjoitetaan antiikvalla: sin x, logax.
(Johdonmukaista, mutta ei tavanomaista olisi lisätä näihin sulut: sin(x),
loga(x).)
)/(2a), f(x).
Standardifunktioiden nimet sen sijaan kirjoitetaan antiikvalla: sin x, logax.
(Johdonmukaista, mutta ei tavanomaista olisi lisätä näihin sulut: sin(x),
loga(x).)
Vektorit merkitään joko lihavoituina, a, tai merkitsemällä viiva tai nuoli symbolin
päälle, 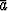 ,
, 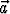 .
.
Erikoistilanteissa käytetään myös esimerkiksi kaunokirjoitus-, fraktuura- tai muita
symboleja: A, 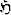 ,
,  .
.
Kreikkalaiset kirjaimet ovat varsin laajassa käytössä osoittamassa esimerkiksi kulmien suuruuksia tai usein skalaareja (vektorin vastakohtana).
![[#]](kuvat/msam10-c-4.gif) geometria geometria![[#]](kuvat/msam10-c-4.gif) geometria geometria![[#]](kuvat/msam10-c-4.gif) algebra algebra![[#]](kuvat/msam10-c-4.gif) Newton Newton![[#]](kuvat/msam10-c-4.gif) Leibniz Leibniz![[#]](kuvat/msam10-c-4.gif) Euler Euler![[#]](kuvat/msam10-c-4.gif) pii pii![[#]](kuvat/msam10-c-4.gif) Neperin
luku Neperin
luku![[#]](kuvat/msam10-c-4.gif) imaginaariyksikkö imaginaariyksikkö |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12