![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometrian peruskäsitteet
Geometrian peruskäsitteet  Vektorialgebra [
1 2 3 4 5 ]
Vektorialgebra [
1 2 3 4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) vektori
vektori
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) determinantti
determinantti
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Geometrian peruskäsitteet Geometrian peruskäsitteet  Vektorialgebra [
1 2 3 4 5 ] Vektorialgebra [
1 2 3 4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) vektori vektori
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) determinantti determinantti
|
|
Kolmesta vektorista muodostettu tulo a . b × c on mielekäs vain, mikäli vektoritulo lasketaan ennen skalaarituloa: a . (b × c). Tuloksena on skalaari ja tuloa kutsutaankin skalaarikolmituloksi. Sulut on tapana jättää pois, koska lausekkeella on vain yksi mielekäs tulkinta.
Skalaari- ja vektoritulon lausekkeiden perusteella voidaan mekaanisella laskulla osoittaa, että skalaarikolmitulossa voidaan pisteen ja ristin paikkaa vaihtaa ja toisaalta tekijävektoreita kierrättää ilman että tulon arvo muuttuu:
| a . b × c = a × b . c, |
| a . b × c = b . c × a = c . a × b. |
Jos tekijöistä kaksi vaihdetaan keskenään, muuttuu skalaarikolmitulon merkki: esimerkiksi a . b × c = -b . a × c. Jos kaksi (tai kolme) tekijää on samoja, tulo on = 0.
Skalaarikolmitulo voidaan myös laskea determinantista:
a . b × c = 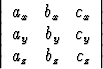 ,
,
missä a = axi + ayj + azk, b = bxi + byj + bzk ja c = cxi + cyj + czk.
Kolmesta vektorista muodostettu kaksinkertainen vektoritulo on myös mielekäs: a × (b × c) tai (a × b) × c. Tämän arvo on vektori ja sitä kutsutaan vektorikolmituloksi.
Vektorikolmitulolle on voimassa kehityskaavat
| a × (b × c) = (a . c)b - (a . b)c, |
| (a × b) × c = (c . a)b - (c . b)a. |
![[#]](kuvat/msam10-c-4.gif) vektori vektori![[#]](kuvat/msam10-c-4.gif) skalaari skalaari![[#]](kuvat/msam10-c-4.gif) determinantti determinantti |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12