![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometrian peruskäsitteet
Geometrian peruskäsitteet  Vektorialgebra [
1 2 3 4 5 ]
Vektorialgebra [
1 2 3 4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) vektori
vektori
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) determinantti
determinantti
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Geometrian peruskäsitteet Geometrian peruskäsitteet  Vektorialgebra [
1 2 3 4 5 ] Vektorialgebra [
1 2 3 4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) vektori vektori
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) determinantti determinantti
|
|
Kantavektoreiden vektoritulot ovat
| i × i = j × j = k × k = o, |
| i × j = k, j × k = i, k × i = j ja |
| j × i = -k, k × j = -i, i × k = -j. |
Vektoreiden a = axi + ayj + azk ja b = bxi + byj + bzk vektorituloksi saadaan tällöin
| a × b | = |
| ||||||||||||||||||||
| = | (aybz - azby)i + (azbx - axbz)j + (axby - aybx)k. |
a × b = 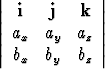 .
.
![[#]](kuvat/msam10-c-4.gif) kantavektori kantavektori![[#]](kuvat/msam10-c-4.gif) determinantti determinantti |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12