Galtonin fortuna-lauta
Englantilainen luonnontutkija ja tilastotieteilijä F. Galton rakensi 1800-luvulla eräänlaisen
fortuna-laudan. Laudassa esteet sijoitetaan kuvan osoittamalla tavalla. Lautaa alas
vierivä kuula osuu jokaisella esterivillä yhteen esteeseen. Jokaisesta esteestä
kuulalla on yhtä suuri mahdollisuus vieriä joko esteen oikealta tai vasemmalta
puolelta. Kuulan sattumanvarainen kulku päättyy aina johonkin alhaalla olevista
karsinoista.
Millä todennäköisyydellä kuula vierii jompaan kumpaan keskimmäisistä karsinoista, kun
karsinoita on kuvan mukaisesti yhteensä kymmenen?
Ratkaisu
Jos laudalle merkitään esteiden väliin numerot, jotka ilmoittavat kyseiseen väliin
johtavien reittien lukumäärät, saadaan seuraavan näköinen tutulta näyttävä kolmio, joka
on Pascalin kolmio:
| | | | | | | | | | 1 | | | | | | | | | |
| | | | | | | | | 1 | | 1 | | | | | | | | |
| | | | | | | | 1 | | 2 | | 1 | | | | | | | |
| | | | | | | 1 | | 3 | | 3 | | 1 | | | | | | |
| | | | | | 1 | | 4 | | 6 | | 4 | | 1 | | | | | |
| | | | | 1 | | 5 | | 10 | | 10 | | 5 | | 1 | | | | |
| | | | 1 | | 6 | | 15 | | 20 | | 15 | | 6 | | 1 | | | |
| | | 1 | | 7 | | 21 | | 35 | | 35 | | 21 | | 7 | | 1 | | |
| | 1 | | 8 | | 28 | | 56 | | 70 | | 56 | | 28 | | 8 | | 1 | |
| 1 | | 9 | | 36 | | 84 | | 126 | | 126 | | 84 | | 36 | | 9 | | 1 |
| |
|
Kahteen keskimmäiseen karsinaan johtaa siten yhteensä 252 eri reittiä. Kuula voi vieriä
kaikkiin karsinoihin yhteensä 512 eri reittiä pitkin. Todennäköisyys, että kuula vierii
keskimmäisiin karsinoihin, on siis
 =
= 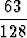 = 0.4922.
= 0.4922.
Jos suuren määrän kuulia annetaan vieriä pitkin lautaa, karsinoihin vierineet kuulat
muodostavat yhdessä varsin säännönmukaisen kasan. Kuulia kertyy kasoihin likimain
niiden lukujen suhteessa, jotka saadaan Pascalin kolmion kymmenenneltä riviltä. Jos
Galtonin lautaa suurennetaan siten, että karsinoita on enemmän ja lisäksi kuulia
vieritetään suuri määrä, kuulien karsinoihin muodostamien kasojen muoto alkaa
muistuttaa kellokäyrää.


 =
= 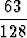 = 0.4922.
= 0.4922.