
Kottikärryn pohja on suorakulmio, jonka sivut ovat 23 cm ja 20 cm. Laitatasoista kolme muodostaa pohjatason kanssa 120o kulman ja toinen lyhyemmän pohjasivun vastaisista laitatasoista 135o kulman kärryn sisäpuolelta katsottuna. Kärryn reunat muodostavat suorakulmion, joka on pohjan suuntaisessa, pohjasta etäisyydellä 30 cm sijaitsevassa tasossa. Laske kärryn tilavuus.

|
A(vj) = (23 + vjtan 30o + vjtan 45o) . (20 + 2vjtan 30o).
Jos tässä kohdassa olevan viipaleen paksuus on zj, viipaleen tilavuus on A(vj)
zj, viipaleen tilavuus on A(vj) zj.
Koko kärryn tilavuutta approksimoi Riemannin summa
zj.
Koko kärryn tilavuutta approksimoi Riemannin summa
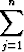 A(vj)
A(vj) zj,
zj,
 A(z) dz A(z) dz | =  (23 + z + (23 + z +  ) . (20 + ) . (20 +  ) dz ) dz |
= 20 . 23 . 30 +  . 20 . 302 + . 20 . 302 +  . . 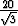 . 302 . 302 |
|
+ . .  . 302 + . 302 +  . . 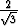 . 303 + . 303 +  . .  . 303 . 303 |
|
| = 56340. |
Laske kottikärryn tilavuus myös paloittelemalla kärry sopiviin monitahokkaisiin. Vertaa monitahokkaiden tilavuuksia integraalista saatuihin summattaviin.
Huom! Kottikärryn tilavuutta ei voida laskea käyttäen katkaistun pyramidin kaavaa, sillä kottikärry ei ole katkaistu pyramidi!
| Piilota ratkaisu |