Tienmutkan jyrkkyys
Oletetaan, että maantiessä oleva mutka on peruskartalla käyrän
y = 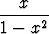 , -1 < x < 1,
, -1 < x < 1,
muotoinen, yksikkönä senttimetri. Tien kaarevuussäde kohdassa x voidaan laskea
lausekkeesta
R(x) = 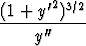 .
.
Peruskartan mittakaava on 1:20 000. Mikä on kaarevuussäteen pienin arvo, ts. arvo siinä
kohdassa, missä tie kaartuu jyrkimmin?
Vihje 1
Kyseessä on ääriarvotehtävä, jossa laskut ovat sen verran hankalat, että jonkin
symbolisia lausekkeita käsittelevän laskentaohjelman käyttö on tarpeen. Piirrä
aluksi kuvio tiestä siten, että yksiköt koordinaattiakseleilla ovat yhtä pitkät.
Vihje 2
Derivoi y kahdesti ja sijoita derivaatat kaarevuussäteen R(x) lausekkeeseen;
sievennä. Tämän funktion minimi on siis haettava. Derivoi, sievennä, laske derivaatan
nollakohta. Näitä on oleellisesti yksi. Hyödynnä laskentaohjelman tarjoamat
mahdollisuudet.
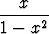 , -1 < x < 1,
, -1 < x < 1,
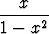 , -1 < x < 1,
, -1 < x < 1,
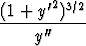 .
.