Tienmutkan jyrkkyys
Oletetaan, että maantiessä oleva mutka on peruskartalla käyrän
y = 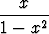 , -1 < x < 1,
, -1 < x < 1,
muotoinen, yksikkönä senttimetri. Tien kaarevuussäde kohdassa x voidaan laskea
lausekkeesta
R(x) = 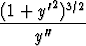 .
.
Peruskartan mittakaava on 1:20 000. Mikä on kaarevuussäteen pienin arvo, ts. arvo siinä
kohdassa, missä tie kaartuu jyrkimmin?
Vihje 1
Kyseessä on ääriarvotehtävä, jossa laskut ovat sen verran hankalat, että jonkin
symbolisia lausekkeita käsittelevän laskentaohjelman käyttö on tarpeen. Piirrä
aluksi kuvio tiestä siten, että yksiköt koordinaattiakseleilla ovat yhtä pitkät.
Vihje 2
Derivoi y kahdesti ja sijoita derivaatat kaarevuussäteen R(x) lausekkeeseen;
sievennä. Tämän funktion minimi on siis haettava. Derivoi, sievennä, laske derivaatan
nollakohta. Näitä on oleellisesti yksi. Hyödynnä laskentaohjelman tarjoamat
mahdollisuudet.
Vihje 3
Kovin sieviä lausekkeita ei synny, mutta älä anna sen häiritä. Nollakohdan
algebrallinen ratkaisu tuskin onnistuu. Yritä graafisesti tai numeerisesti. Ohjelma tarjoaa
tähänkin keinot. Saattaa olla tarpeen miettiä, mikä tekijä derivoidun kaarevuussäteen
lausekkeessa antaa nollakohdan, ja sen jälkeen tutkia tätä tekijää erikseen.
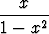 , -1 < x < 1,
, -1 < x < 1,
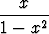 , -1 < x < 1,
, -1 < x < 1,
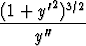 .
.