1 Topologiaa
1.1 Ympäristö
1.2 Topologisia peruskäsitteitä
Tehtävä 1
Määritä seuraavien reaalilukujoukkojen kasautumispisteet:
a) 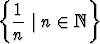 , b)
, b) 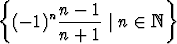 .
.
Tehtävä 2
Reaalilukujoukoilla S ja T olkoon seuraava ominaisuus:
x  S
S 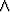 y
y  T
T 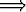 |x - y| > c,
|x - y| > c,
missä c on positiivinen vakio. Todista, että joukoilla S ja T ei ole yhtään yhteistä kasautumispistettä.
Tehtävä 3
Olkoon S reaalilukujoukko ja sup S = G. Todista, että jos G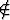 S, niin G on
joukon S kasautumispiste.
S, niin G on
joukon S kasautumispiste.
Tehtävä 4
Tutki, ovatko seuraavat joukot Sk avoimia tai suljettuja (tai ei kumpiakaan). Määritä joukkojen sisäpisteet, reunapisteet ja kasautumispisteet.S1 = ] - 1, 0[ 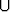 ]0, 1] ]0, 1] 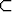  , , | S2 = {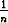 | n | n   } } 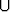 {0} {0} 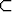  , , | ||||||
S3 = 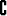 (S2 ) (S2 ) 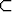  , , | S4 = {(x, y) | x  [a, b], y [a, b], y  [c, d]} [c, d]} 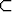  2, 2, | ||||||
S5 = {(x, y) | |x| + |y| = 1} 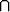 {(x, y) | y {(x, y) | y  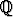 } } 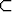  2, 2, | S6 = {(x, y) | x + y  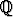 } } 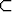  2, 2, | ||||||
S7 = {(x, y, z) | xyz > 0} 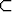  3. 3. |
Tehtävä 5
Todista, että joukko S on avoin, jos ja vain jos se on muotoa U (x) olevien
ympäristöjen unioni.
(x) olevien
ympäristöjen unioni.
Tehtävä 6
Todista, että avoimien joukkojen unioni on avoin.Tehtävä 7
Anna esimerkki, joka osoittaa, että suljettujen joukkojen unioni ei välttämättä ole suljettu.Tehtävä 8
Jos joukkoon S liitetään sen kasautumispisteet, saadaan joukon S sulkeuma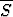 .
Osoita:
.
Osoita: 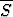 = S
= S 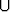
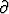 S.
S.
Tehtävä 9
Jos joukkoon S liitetään sen kasautumispisteet, saadaan joukon S sulkeuma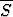 .
Osoita: a) S
.
Osoita: a) S 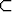 T
T 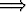
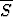
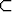
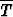 , b)
, b) 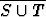 =
= 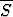
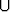
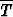 .
.
Tehtävä 10
Todista, että joukon reuna on suljettu joukko.Tehtävä 11
Todista, että suljetun joukon reuna kuuluu itse joukkoon, ts. jos S on suljettu joukko, niin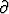 S
S 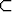 S.
S.
Tehtävä 12
Jos joukkoon S liitetään sen kasautumispisteet, saadaan joukon S sulkeuma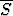 . Todista:
. Todista: 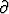
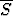
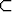
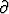 S. Anna esimerkki, jossa
S. Anna esimerkki, jossa 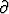
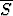 on reunan
on reunan 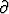 S aito osajoukko.
S aito osajoukko.
Tehtävä 13
Todista, että joukon kasautumispisteiden muodostama joukko on suljettu.Tehtävä 14
Olkoon S tason 2 joukko. Osoita, että joukko {
2 joukko. Osoita, että joukko {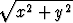 | (x, y)
| (x, y)  S}
S} 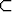
 on rajoitettu, jos ja vain jos joukot {x |
on rajoitettu, jos ja vain jos joukot {x | 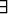 y siten, että (x, y)
y siten, että (x, y)  S}
S} 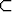
 ja
{y |
ja
{y | 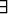 x siten, että (x, y)
x siten, että (x, y)  S}
S} 
 ovat rajoitettuja. Onko joukko S
ovat rajoitettuja. Onko joukko S 
 2 tällöin itse
rajoitettu?
2 tällöin itse
rajoitettu?