2 Lukujonot
2.1 Lukujonon määritelmä
Tehtävä 16
Fibonacci’n luvut määritellään ehdoilla
a1 = a2 = 1; an+2 = an+1 + an, n 
 .
.
Osoita:
an = 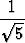
![[( V~ -)n ( V~ -)n]
1 +---5 - 1----5-
2 2](kuvat/ra19x.gif) .
.
Tehtävä 17
Olkoon a1 = 3, a2 = 6, an+1 =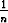 (nan + an-1 + 3) arvoilla n > 2. Todista, että
an < 4n kaikilla n
(nan + an-1 + 3) arvoilla n > 2. Todista, että
an < 4n kaikilla n 
 .
.
Tehtävä 18
Määritä inf{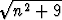 - n/2 | n
- n/2 | n 
 }.
}.
2.2 Lukujonon suppeneminen
Tehtävä 19
Määritä lukujonon
an = 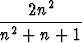
raja-arvo, kun n 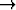
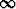 , ja todista tulos suoraan määritelmän perusteella (ts.
epsilontekniikkaa käyttäen).
, ja todista tulos suoraan määritelmän perusteella (ts.
epsilontekniikkaa käyttäen).
Tehtävä 20
Todista raja-arvon määritelmään perustuen, että suppeneva lukujono on rajoitettu, ts. jos lim an = a, niin on olemassa luku M > 0 siten, että |an| < M kaikilla indekseillä n.Tehtävä 21
Todista raja-arvon määritelmään perustuen seuraava lause: Jos lukujonolle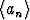 pätee lim an = a ja lim an = b, niin a = b.
pätee lim an = a ja lim an = b, niin a = b.
Tehtävä 22
Todista yksityiskohtaisesti lukujonojen raja-arvoja koskeva lause: Jos limn
 an = a ja limn
an = a ja limn
 bn = b, niin limn
bn = b, niin limn
 (an + bn) = a + b. Päteekö
kääntäen
(an + bn) = a + b. Päteekö
kääntäen
limn
 (an + bn) = a + b
(an + bn) = a + b 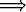 limn
limn
 an = a, limn
an = a, limn
 bn = b ?
bn = b ?
Tehtävä 23
Todista: Jos lukujonolle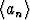 pätee an > 0 kaikilla indekseillä n
pätee an > 0 kaikilla indekseillä n 
 ja
liman = 0, niin on olemassa max{ an | n
ja
liman = 0, niin on olemassa max{ an | n 
 }. Onko em. oletuksilla välttämättä olemassa
myös min { an | n
}. Onko em. oletuksilla välttämättä olemassa
myös min { an | n 
 }?
}?
Tehtävä 24
Olkoon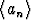 rajoitettu lukujono. Todista:
rajoitettu lukujono. Todista:
limn

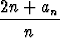 = 2.
= 2.
Tehtävä 25
Olkoon
limn

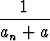 = b
= b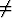 0.
0.
Osoita täsmällisesti, että lukujono 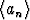 suppenee ja määritä sen raja-arvo.
suppenee ja määritä sen raja-arvo.
Tehtävä 26
Määritä raja-arvota) limn  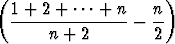 , , | b) limn  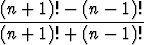 , , | ||||||
c) limn  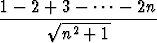 , , | d) limn  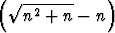 . . |
Tehtävä 27
Määritä raja-arvo limn
 fn(x) = f(x) kaikilla arvoilla x
fn(x) = f(x) kaikilla arvoilla x 
 ,
kun
,
kun
fn(x) = 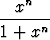 .
.
Piirrä funktioiden fn kuvaajia indeksin n eri arvoilla. Piirrä myös funktion f kuvaaja.
Tehtävä 28
Määritä raja-arvo limn
 fn(x) = f(x) kaikilla arvoilla x
fn(x) = f(x) kaikilla arvoilla x 
 ,
kun
,
kun
fn(x) = 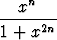 .
.
Piirrä funktioiden fn kuvaajia indeksin n eri arvoilla. Piirrä myös funktion f kuvaaja.
Tehtävä 29
Osoita, että lukujono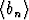 ,
,
bn = 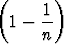 n,
n,
on kasvava ja ylhäältä rajoitettu. Käytä Bernoulli’n epäyhtälöä. Mikä on jonon raja-arvo?
Tehtävä 30
Olkoon lim an = a. Osoita:
lim 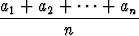 = a.
= a.
Tehtävä 31
Olkoot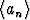 ja
ja 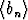 kaksi lukujonoa, joille pätee lim(anen) = e ja
lim(bn n-10 ) =
kaksi lukujonoa, joille pätee lim(anen) = e ja
lim(bn n-10 ) =  . Määritä lim(anbn), mikäli se on olemassa.
. Määritä lim(anbn), mikäli se on olemassa.
Tehtävä 32
Lukujono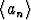 määritellään asettamalla
määritellään asettamalla
a1 = 1; an+1 = 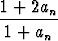 , n = 1, 2, 3, . . . .
, n = 1, 2, 3, . . . .
Osoita induktiolla, että jono on ylhäältä rajoitettu ja kasvava. Päättele tästä, että jonon raja-arvo on olemassa ja laske se.
Tehtävä 33
Lukujono määritellään rekursiivisesti ehdoilla a1 = 0, an+1 = an + 1. Osoita,
että jono on kasvava ja ylhäältä rajoitettu. Määritä sen raja-arvo.
an + 1. Osoita,
että jono on kasvava ja ylhäältä rajoitettu. Määritä sen raja-arvo.
Tehtävä 34
Lukujono määritellään rekursiivisesti ehdoilla
a1 = 1, an+1 = 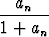 .
.
Osoita, että jono on vähenevä ja alhaalta rajoitettu. Määritä sen raja-arvo.
Tehtävä 35
Lukujono määritellään rekursiivisesti ehdoilla
a1 = 0, an+1 = 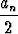 + 5.
+ 5.
Osoita täsmällisesti, että jono suppenee ja määritä sen raja-arvo.
Tehtävä 36
Osoita seuraavat jonot monotonisiksi ja rajoitetuiksi sekä määritä niiden raja-arvot:
a) a1 = 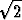 , an+1 =
, an+1 = 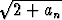 , b) a1 =
, b) a1 = 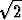 , an+1 =
, an+1 = 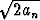 .
.
Tehtävä 37
Olkoon a1 ]0,
]0,  /2[ ja an+1 = sin an (n > 1). Osoita jono väheneväksi ja
alhaalta rajoitetuksi sekä määritä sen raja-arvo.
/2[ ja an+1 = sin an (n > 1). Osoita jono väheneväksi ja
alhaalta rajoitetuksi sekä määritä sen raja-arvo.
Tehtävä 38
Tutki numeerisesti raja-arvoa
limn
 (1 + 1/n)n
(1 + 1/n)n
sijoittamalla luvulle n yhä suurempia arvoja.
Tehtävä 39
Tutki numeerisesti raja-arvoja
a) limn

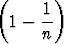 n, b) limn
n, b) limn

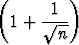 n, c) limn
n, c) limn

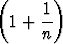
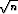 .
.
Mitkä ovat raja-arvojen tarkat arvot? Miten tulokset voi perustella?
2.3 Cauchyn suppenemiskriteeri
Tehtävä 40
Tutki seuraavien lukujonojen käyttäytymistä:
a) an = cos 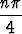 + (-1)n, b) an = sin
+ (-1)n, b) an = sin 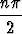 +
+ 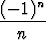 .
.
Onko jonoilla raja-arvoa? Entä kasautumispisteitä? Mitä mahdettaisiin tarkoittaa käsitteillä yläraja-arvo ja alaraja-arvo (limes superior ja limes inferior)?
Tehtävä 41
Osoita, että lukujono an = 1/n (n
 ) toteuttaa Cauchyn suppenemisehdon,
ts. määritä annettua lukua
) toteuttaa Cauchyn suppenemisehdon,
ts. määritä annettua lukua  > 0 vastaava indeksiraja N.
> 0 vastaava indeksiraja N.
Tehtävä 42
Lukujonolla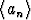 olkoon ominaisuudet
olkoon ominaisuudet
1) i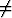 j
j 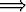 ai
ai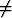 aj, 2)
aj, 2)  lim an = a
lim an = a 
 .
.
Todista, että a on lukujoukon {an | n 
 }
} 
 kasautumispiste. Voiko joukolla olla
muita kasautumispisteitä? Jos ominaisuudesta 1) luovutaan, pitääkö väite paikkansa?
kasautumispiste. Voiko joukolla olla
muita kasautumispisteitä? Jos ominaisuudesta 1) luovutaan, pitääkö väite paikkansa?