3 Funktion raja-arvo ja jatkuvuus
3.1 Reaali- ja kompleksifunktiot
Tehtävä 43
Olkoon f monotoninen ja rajoitettu välillä ]a, b[. Todista, että raja-arvot limx a+f(x) ja limx
a+f(x) ja limx b-f(x) ovat olemassa. Todista myös, että limx
b-f(x) ovat olemassa. Todista myös, että limx c-f(x) ja
limx
c-f(x) ja
limx c+f(x) ovat olemassa, kun c
c+f(x) ovat olemassa, kun c  ]a, b[.
]a, b[.
Tehtävä 44
Todista monotonisuuden määritelmään nojautuen, että seuraavat funktiot ovat monotonisia mainitulla välillä: a) x3 + 3x - 3, x
 , b)
, b) 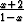 , x
, x  ]1,
]1, 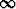 [.
[.
Tehtävä 45
Olkoot f ja g kasvavia välillä I. Todista, että f + g on kasvava välillä I.Tehtävä 46
Olkoot f ja g kasvavia välillä I. Todista, että h(x) = max{f(x), g(x)} on kasvava välillä I.Tehtävä 47
Olkoon f aidosti kasvava joukossa + = {x
+ = {x 
 | x > 0} ja limx
| x > 0} ja limx 0+f(x) = 0.
Todista: x > 0
0+f(x) = 0.
Todista: x > 0 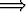 f(x) > 0.
f(x) > 0.
Tehtävä 48
Osoita, että jos funktiot f ja g ovat parillisia, niin myös f + g ja fg ovat parillisia. Osoita edelleen, että jos f ja g ovat parittomia, niin f + g on pariton ja fg parillinen.Tehtävä 49
Funktio f olkoon määritelty reaaliakselin välillä ] - a, a[. Todista, että f voidaan kirjoittaa muotoon f = f1 + f2, missä f1 on parillinen ja f2 pariton funktio.Tehtävä 50
Olkoon L reaalimuuttujan funktion f jakso. Mitä muita jaksoja funktiolla on?Tehtävä 51
Olkoon f1(x) = x + 1, f2(x) = x - 2, f3(x) = 2x + 3, f4(x) = x2 + x. Muodosta seuraavat yhdistetyt funktiot: a) f4(f3(f2(x))), b) f2(f3(f4(x))), c) f4 (f1 (f1 (x3 ))).Tehtävä 52
Olkoon f(x) = ax2 + bx + c. Määritä a, b ja c siten, että f(x + 2) = f(x) + 2 kaikilla x
 .
.
Tehtävä 53
Piirrä seuraavien funktioiden kuvaajat:a) f(x) = 1 + x - |x|, b) f(x) = |x + 1| + |x - 1| - 2|x|, c) f(x) = |x2 - 1| - x2.
3.2 Funktion raja-arvo
Tehtävä 54
Todista suoraan raja-arvon määritelmään nojautuen, että limx 10x2 = 100.
10x2 = 100.
Tehtävä 55
Todista suoraan raja-arvon määritelmään perustuen, että limx a
a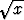 =
= 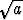 (a > 0), ts. etsi annettua lukua
(a > 0), ts. etsi annettua lukua  vastaava
vastaava 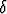 .
.
Tehtävä 56
Todista, että limx af(x) = A, jos ja vain jos limx
af(x) = A, jos ja vain jos limx a[f(x) - A] = 0.
a[f(x) - A] = 0.
Tehtävä 57
Olkoon f(x) < g(x) < h(x) pisteen a aidossa ympäristössä sekä lisäksi limx af(x) = limx
af(x) = limx ah(x) = A. Todista, että limx
ah(x) = A. Todista, että limx ag(x) = A.
ag(x) = A.
Tehtävä 58
Olkoon limx af(x) = 0 ja olkoon g(x) rajoitettu eräässä pisteen a
ympäristössä. Todista:
af(x) = 0 ja olkoon g(x) rajoitettu eräässä pisteen a
ympäristössä. Todista:
limx a(f(x)g(x)) = 0.
a(f(x)g(x)) = 0.
Tehtävä 59
Olkoon limx af(x) = A
af(x) = A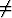 0 ja älköön limx
0 ja älköön limx ag(x) olko olemassa. Todista,
että limx
ag(x) olko olemassa. Todista,
että limx a (f(x)g(x)) ei ole olemassa.
a (f(x)g(x)) ei ole olemassa.
Tehtävä 60
Määritä seuraavat raja-arvot:a) limx 1 1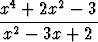 , , | b) limx 1 1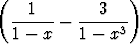 , , | ||||||
c) limx 2 2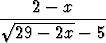 , , | d) limx 0 0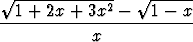 | ||||||
e) limx 9 9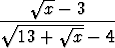 , , | f) limx 0 0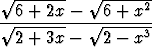 . . |
Tehtävä 61
Määrittele täsmällisestia) limx - - f(x) = A, f(x) = A, | b) limx - - f(x) = f(x) = 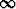 , , | c) limx af(x) = - af(x) = -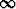 , , | |||||||||
d) limx  f(x) = - f(x) = -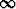 , , | e) limx  f(x) = f(x) = 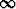 . . |
Tehtävä 62
Etsi jokaista positiivilukua kohti jokin luku M siten, että
kohti jokin luku M siten, että
x > M 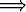
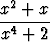 <
<  .
.
Tehtävä 63
Määritä inf S, kun
S = 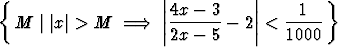 .
.
Mitä tekemistä tällä on raja-arvon määritelmän kanssa?
Tehtävä 64
Olkoon a
 , A
, A 
 . Todista seuraavat raja-arvoa koskevat tulokset suoraan
määritelmään perustuen:
. Todista seuraavat raja-arvoa koskevat tulokset suoraan
määritelmään perustuen:
a) limx af(x) = A af(x) = A | ja limx ag(x) = ag(x) = 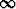 | 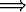 limx limx a(f(x) + g(x)) = a(f(x) + g(x)) = 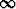 , , | |||||||||
b) limx  f(x) = f(x) = 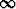 | ja limx  g(x) = - g(x) = -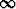 | 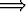 limx limx  (f(x)g(x)) = - (f(x)g(x)) = -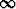 , , | |||||||||
c) limx - - f(x) = A f(x) = A | ja limx - - g(x) = g(x) = 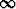 |  limx limx - -  = 0. = 0. |
Tehtävä 65
Todista, että jos toinen raja-arvoista limx
 f(x) ja limx
f(x) ja limx 0+f(1/x) on
olemassa, niin on toinenkin ja raja-arvot ovat yhtä suuret.
0+f(1/x) on
olemassa, niin on toinenkin ja raja-arvot ovat yhtä suuret.
Tehtävä 66
Määritä seuraavat raja-arvot:a) limx - - 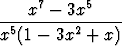 , , | b) limx  ( (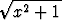 - x), - x), | ||||||
c) limx  ( (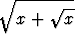 - - 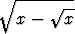 ), ), | d) limx 7- 7-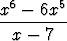 , , | ||||||
e) limx 5- 5-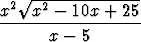 , , | f) limx 5+ 5+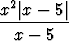 . . |
Tehtävä 67
Määritäa) limx  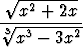 , , | b) limx 0 0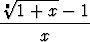 , , | ||||||
c) limx -1 -1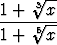 , , | d) limx a+ a+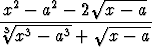 . . |
Tehtävä 68
Olkoon
f(x) = limy

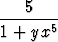 .
.
Osoita, että limx 0f(x) = 0.
0f(x) = 0.
Tehtävä 69
Olkoon ABCD 0. Määritä
0. Määritä
limy

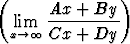 - limx
- limx

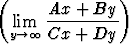 .
.
Tehtävä 70
Tutki numeerisesti raja-arvoa
limx 9
9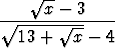 .
.
Tehtävä 71
Tutki raja-arvoa
limx 0
0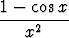
sijoittamalla muuttujalle x yhä lähempänä origoa olevia arvoja.
Tehtävä 72
Tutki raja-arvoa
limx
 (sin x)tan 2
x
(sin x)tan 2
x
sijoittamalla muuttujalle x yhä lähempänä origoa olevia arvoja.
Tehtävä 73
Piirrä funktiony(x) = (sin x)tan 2 x
kuvaaja pisteen 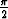 ympäristössä. Miten funktion arvo tässä pisteessä on määriteltävä,
jotta siitä tulisi jatkuva? Mikä mahtaa olla raja-arvon tarkka arvo?
ympäristössä. Miten funktion arvo tässä pisteessä on määriteltävä,
jotta siitä tulisi jatkuva? Mikä mahtaa olla raja-arvon tarkka arvo?
Tehtävä 74
Hahmottele funktioiden
sin 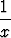 ja x sin
ja x sin 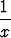
kuvaajat, ja tutki funktioiden raja-arvoja origossa.
Tehtävä 75
Määritellään reaalimuuttujan reaaliarvoiset funktiot f ja g seuraavasti:
f(x) =  g(x) =
g(x) = 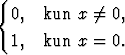
Määritä funktioiden raja-arvot origossa. Onko yhdistetyllä funktiolla gof raja-arvoa origossa?
3.3 Funktion jatkuvuus
Tehtävä 76
Funktio
f(x) = 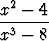
on määritelty, kun x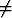 2. Mikä on sovittava f(2):n arvoksi, jotta funktio olisi jatkuva
kaikilla muuttujan x
2. Mikä on sovittava f(2):n arvoksi, jotta funktio olisi jatkuva
kaikilla muuttujan x 
 arvoilla?
arvoilla?
Tehtävä 77
Olkoona) f(x) =  | |||
b) f(x) = 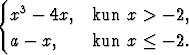 |
Määritä ne a:n arvot, joilla vastaava f on jatkuva kaikilla muuttujan x 
 arvoilla. Piirrä
kuvaajat.
arvoilla. Piirrä
kuvaajat.
Tehtävä 78
Olkoon f jatkuva arvolla x = 0 ja f(0) > 0. Osoita, että on olemassa positiiviluvut m ja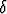 siten, että |x| <
siten, että |x| < 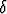
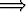 f(x) > m.
f(x) > m.
Tehtävä 79
Todista, että jos f on jatkuva ja g on epäjatkuva, kun x = a, niin f + g on epäjatkuva tässä pisteessä.Tehtävä 80
Todista, että jos pisteessä x = a funktio f on jatkuva ja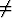 0 sekä g
epäjatkuva, niin tulo fg on epäjatkuva.
0 sekä g
epäjatkuva, niin tulo fg on epäjatkuva.
Tehtävä 81
Määritellään funktio floor :
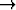
 asettamalla
asettamalla
floor(x) = suurin kokonaisluku, joka on < x.
Olkoon f tämän avulla määritelty funktio:
f(x) = floor(x) + floor(-x) + 1.
Tutki funktioiden floor ja f jatkuvuutta. Piirrä funktioiden kuvaajat. Ovatko funktiot jaksollisia?
Tehtävä 82
Määritä sup S, kun
S = 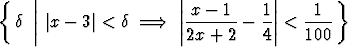 .
.
Mitä tekemistä tällä tehtävällä on funktion jatkuvuuden kanssa?
Tehtävä 83
Funktio f olkoon määritelty ja aidosti kasvava välillä [a, b]. Funktion arvojoukko olkoon väli [f(a), f(b)]. Osoita, että funktio on jatkuva.Tehtävä 84
Olkoon funktio f jatkuva välillä ] - 1, 1[ ja f(0) = 0. Funktio g olkoon määritelty (mutta ei välttämättä jatkuva) samalla välillä ja se toteuttakoon tällä välillä ehdon g(x) > m > 0, missä m on vakio. Osoita, että funktio f/g on jatkuva origossa. Osoita esimerkillä, että tulos ei välttämättä pidä paikkaansa, jos funktiota g koskeva ehto muutetaan muotoon g(x) > 0. (Valitse esimerkiksi f(x) = x ja tämän jälkeen sopiva origossa epäjatkuva g.)Tehtävä 85
Etsi seuraavien funktioiden käänteisfunktioiden lausekkeet:
a) y = 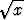 +
+ 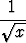 , b) y =
, b) y = 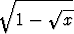 +
+ 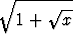 .
.
Tehtävä 86
Osoita, että jos
y = f(x) = 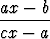 ,
,
niin x = f(y). Oletetaan, että a2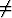 bc. Miksi?
bc. Miksi?
Tehtävä 87
Olkoon A = { x
 | x < 0 tai x > 1 } ja B = { y
| x < 0 tai x > 1 } ja B = { y 
 | 0 < y < 2 }. Osoita,
että funktio f : A
| 0 < y < 2 }. Osoita,
että funktio f : A  B,
B,
f(x) = 
on jatkuva bijektio, mutta sen käänteisfunktio ei ole jatkuva.
Tehtävä 88
Olkoon f joukossa + aidosti kasvava ja jatkuva sekä olkoon limx
+ aidosti kasvava ja jatkuva sekä olkoon limx 0+f(x) = 0.
Olkoon y = g(x) = xf(x) kaikilla x > 0. Osoita, että funktiolla g on arvoilla y > 0
määritelty käänteisfunktio.
0+f(x) = 0.
Olkoon y = g(x) = xf(x) kaikilla x > 0. Osoita, että funktiolla g on arvoilla y > 0
määritelty käänteisfunktio.
3.4 Jatkuvat reaalifunktiot
Tehtävä 89
Todista, että jos funktio f on tasaisesti jatkuva välillä I, niin f on jatkuva välillä I.Tehtävä 90
Osoita tasaisen jatkuvuuden määritelmään nojautuen, että x2 a) on tasaisesti jatkuva välillä [0, 1], b) ei ole tasaisesti jatkuva joukossa {x | x > 0}.Tehtävä 91
Osoita tasaisen jatkuvuuden määritelmään nojautuen, että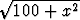 on
tasaisesti jatkuva joukossa
on
tasaisesti jatkuva joukossa  .
.
Tehtävä 92
Todista, että jos funktiot f ja g ovat tasaisesti jatkuvia välillä I, niin f + g on tasaisesti jatkuva välillä I.Tehtävä 93
Anna esimerkki a) avoimella välillä jatkuvasta, ei-rajoitetusta funktiosta, b) suljetulla välillä määritellystä ja rajoitetusta funktiosta, jonka arvojoukolla ei ole maksimia eikä minimiä.Tehtävä 94
Todista, että joukolla
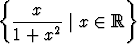
on maksimi ja minimi.
Tehtävä 95
Olkoon funktio f joukossa jatkuva ja rajoitettu. Todista, että
joukolla
jatkuva ja rajoitettu. Todista, että
joukolla
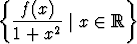
on maksimi tai minimi (tai molemmat).
Tehtävä 96
Osoita esimerkeillä, että seuraavat lauseet eivät päde, jos luovutaan olettamasta, että väli [a, b] on suljettu tai että funktio f on jatkuva:a) Suljetulla välillä [a, b] jatkuva funktio f on tällä välillä rajoitettu, ts. on olemassa luku M > 0, jolle pätee |f(x)| < M kaikilla x
 [a, b].
[a, b].
b) Olkoon f jatkuva suljetulla välillä [a, b]. Tällöin f saavuttaa suuurimman ja pienimmän arvonsa välillä [a, b], ts. on olemassa x1, x2
 [a, b] siten, että
[a, b] siten, että
maxx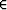 [a,b]f(x) = f(x1), minx
[a,b]f(x) = f(x1), minx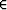 [a,b]f(x) = f(x2).
[a,b]f(x) = f(x2).
Tehtävä 97
Olkoon f suljetulla välillä [a, b] jatkuva funktio, f(a)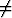 0, f(b) = 0. Todista,
että joukolla { x
0, f(b) = 0. Todista,
että joukolla { x  ]a, b] | f(x) = 0 } on minimi. Päteekö väite, jos sallitaan, että
f(a) = 0?
]a, b] | f(x) = 0 } on minimi. Päteekö väite, jos sallitaan, että
f(a) = 0?
Tehtävä 98
Olkoon funktio f jatkuva suljetulla välillä [a, b]. Osoita, että funktion arvojoukko { f(x) | x [a, b] } on suljettu väli tai sisältää vain yhden pisteen.
[a, b] } on suljettu väli tai sisältää vain yhden pisteen.
Tehtävä 99
Olkoon funktio f jatkuva ja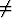 0 välillä I. Osoita, että f saa välillä I vain joko
positiivisia tai negatiivisia arvoja.
0 välillä I. Osoita, että f saa välillä I vain joko
positiivisia tai negatiivisia arvoja.
Tehtävä 100
Osoita, että yhtälöllä x3 - 5x2 + 3 = 0 on ainakin kolme reaalijuurta ja rajoita nämä väleille, joiden pituus on 0.1.Tehtävä 101
Osoita, että yhtälöllä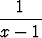 +
+ 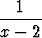 +
+ 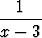 = 0 on ainakin kaksi
reaalijuurta ja rajoita nämä väleille, joiden pituus on 0.1.
= 0 on ainakin kaksi
reaalijuurta ja rajoita nämä väleille, joiden pituus on 0.1.