4 Alkeisfunktiot
4.1 Potenssifunktio
4.2 Polynomit ja rationaalifunktiot
Tehtävä 102
Todista, että jokaisella parittoman asteen reaalikertoimisella polynomilla on ainakin yksi reaalinen nollakohta.Tehtävä 103
Olkoon p(x) = anxn + . . . + a1x + a0 reaalikertoiminen polynomi. Todista, että polynomilla on ainakin yksi reaalinen nollakohta, jos ana0 < 0.Tehtävä 104
Todista, että jos kaksi polynomia, joiden asteluku on < n, saavat samat arvot n eri pisteessä, niin polynimt ovat samat.Tehtävä 105
Todista, että jos astetta n olevalla polynomilla p(x) =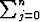 ajxj on kohdissa
xi kertalukua mi olevat nollakohdat (i = 1, 2, . . . , k) ja m1 + m2 + . . . + mk = n, niin
voidaan kirjoittaa
ajxj on kohdissa
xi kertalukua mi olevat nollakohdat (i = 1, 2, . . . , k) ja m1 + m2 + . . . + mk = n, niin
voidaan kirjoittaa
p(x) = an(x - x1)m1 . . . (x - xk)mk .
Tehtävä 106
Olkoot p ja q polynomeja, deg p = n, deg q = m, n > m. Osoita, että on olemassa polynomit h ja r siten, että deg r < deg q ja p = qh + r. Osoita, että nämä ehdot määräävät yksikäsitteisesti polynomit h ja r.Tehtävä 107
Polynomin p asteluku on < 2 ja kaikilla x
 pätee |p(x)| < a|x|3, missä a
on vakio. Osoita, että p(x)
pätee |p(x)| < a|x|3, missä a
on vakio. Osoita, että p(x)  0.
0.
Tehtävä 108
Etsi sen polynomin kertoimet, jonka juurina ovat luvut 1, 2, . . . , 20.Tehtävä 109
Piirrä käyrät
a) y = 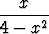 , b) y =
, b) y = 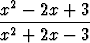 , c) y =
, c) y = 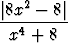
ja määritä niiden asymptootit.
Tehtävä 110
Minkä kahden muuttujan polynomiyhtälön ratkaisuna saadaan seuraava algebrallinen funktio:
a) 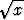 +
+ 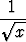 , b)
, b) 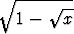 +
+ 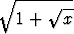 ?
?
4.3 Eksponentti- ja logaritmifunktio
Tehtävä 111
Määritä raja-arvo limx
 x/(ln x)p (p
x/(ln x)p (p 
 ) pitämällä tunnettuna raja-arvoa
limt
) pitämällä tunnettuna raja-arvoa
limt
 et /tp =
et /tp = 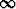 .
.
Tehtävä 112
Määritä raja-arvo limx 0+x(ln x)p (p
0+x(ln x)p (p 
 ) pitämällä tunnettuna raja-arvoa
limt
) pitämällä tunnettuna raja-arvoa
limt
 et /tp =
et /tp = 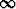 ja sijoittamalla tähän t = - ln x.
ja sijoittamalla tähän t = - ln x.
Tehtävä 113
Määritä raja-arvot
a) limx 0+xx, b) limx
0+xx, b) limx 0+xxx
.
0+xxx
.
Piirrä funktioiden kuvaajat origon oikealla puolella.
Tehtävä 114
Määritä raja-arvo
limy

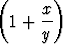 y.
y.
Tehtävä 115
Määritä raja-arvo
limx 0
0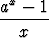 .
.
Tehtävä 116
Olkoot a ja b positiivilukuja. Määritä raja-arvo
limn -
-
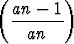
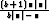 .
.
Tehtävä 117
Määritä ne muuttujan x arvot, joilla käyrän y = ln(1 + ex) ja sen asymptootin ordinaattojen erotus on < ln(1 + e-3).Tehtävä 118
Tutki, millainen xy-tason joukko on { (x, y) | logxy = logyx }. Piirrä kuvio.Tehtävä 119
Osoita: a) logab . logba = 1, b) logba . logcb = logca.Tehtävä 120
Olkoon a > 1. Todista: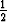 (logax + logay) < loga
(logax + logay) < loga![[1(x + y)]
2](kuvat/ra160x.gif) .
.
Tehtävä 121
Vuotuinen korkoprosentti on 5 ja korko lisätään pääomaan a) jatkuvan koronkoron mukaisesti, b) puolivuosittain. Mikä on eri tavoin saatujen pääomien suhde yhden vuoden kuluttua?Tehtävä 122
Pankkilainan vuotuinen korko on 12 % ja korko maksetaan kerran vuodessa. Laman syvetessä pankki joutuu nostamaan korkoa. Poliittisista syistä korkoprosenttia ei voida nostaa, vaan siirrytään järjestelmään, jossa kertynyt korko kuukausittain liitetään lainapääomaan, minkä jälkeen myös se alkaa kasvaa korkoa. Kuinka monta prosenttia vuosittain kertyvä korko tällöin kasvaa? Selvitä rajaprosessilla, kuinka suureen vuotuisen koron kasvuun on mahdollista päästä, jos kertyvä korko alkaa kasvaa korkoa heti syntyessään.Tehtävä 123
Radioaktiivisen aineen hajoamisessa ainemäärä noudattaa eksponentiaalista vähenemislakia
m(t) = m0e- t,
t,
missä t on aika vuosissa,  aineelle ominainen vakio ja m0 alkuperäinen ainemäärä.
Määritä puoliintumisaika, so. aika, jossa ainemäärä vähenee puoleen, kun
aineelle ominainen vakio ja m0 alkuperäinen ainemäärä.
Määritä puoliintumisaika, so. aika, jossa ainemäärä vähenee puoleen, kun  = 0.02.
= 0.02.
4.4 Trigonometriset funktiot
Tehtävä 124
Tutki, onko yhtälöllä sin(cos x) = cos(sin x) ratkaisuja. Piirrä sopivat kuvaajat ja selvitä asia myös päättelemällä.Tehtävä 125
Määritä seuraavat raja-arvot:a) limx 0 0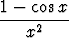 , , | b) limx 0 0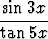 , , | c) limx  x sin x sin 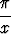 , , | |||||||||
d) limx 0 0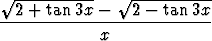 , , | e) limx 0 0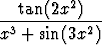 , , | f) limx a a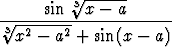 . . |
4.5 Trigonometrian kaavoja
Tehtävä 126
Laadi taulukko, jossa funktiot sin x, cos x, tan x ja cot x ovat lausutut toistensa avulla.Tehtävä 127
Olkoon sin = 7/25 ja cot
= 7/25 ja cot  = -5/12. Laske lausekkeen sin(
= -5/12. Laske lausekkeen sin( -
-  )
mahdolliset arvot.
)
mahdolliset arvot.
Tehtävä 128
Osoita, että kolmion kulmat toteuttavat yhtälöta) sin  + sin + sin  + sin + sin 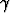 = 4 cos = 4 cos 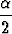 cos cos 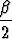 cos cos 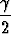 , , | |||
b) tan  + tan + tan  + tan + tan 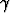 = tan = tan  tan tan  tan tan 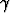 , , | |||
c) cos 2 + cos 2 + cos 2 + cos 2 + cos 2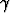 = 1 - cos = 1 - cos  cos cos  cos cos 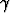 . . |
Tehtävä 129
Ratkaise seuraavat trigonometriset yhtälöt:| a) sin2x = cos 7x, | b) tan 2x = 3 tan x, | c) cos 2x = sin x + cos x, | |||||||||
| d) 4 sin 2 x = tan x, | e) | sin x + | sin x|| = cos x + | cos x|. |
Tehtävä 130
Ratkaise seuraavat trigonometriset epäyhtälöt:a) sin |x| < | sin x|, b) | sin 2x| > | sin 3x|, c) sin 4x > cot x - tan x.
Tehtävä 131
Ratkaise yhtälöparit
a) 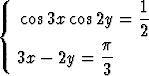 , b)
, b) 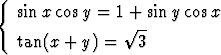 .
.
Tehtävä 132
Missä xy-tason osissa on voimassa sin(x - y) + cos x > 0 ?Tehtävä 133
Määritä raja-arvo
limx
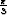
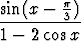 .
.
Tehtävä 134
Olkoon f(x) = sin 2x + x. Määritä jokin luku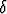 > 0 siten, että
> 0 siten, että
|x1 - x2| < 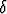
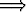 |f(x1) - f(x2)| <
|f(x1) - f(x2)| < 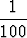 .
.
Miten tehtävä liitty funktion f jatkuvuuteen?
4.6 Harmoninen värähtely
Tehtävä 135
Saata kahden sinivärähtelyn summa a) sin 3x + sin 5x, b) sin 10x + sin 9x muotoon A cos x sin
x sin  x, mikä voidaan tulkita muuttuva-amplitudiseksi sinivärähtelyksi
amplitudina A cos
x, mikä voidaan tulkita muuttuva-amplitudiseksi sinivärähtelyksi
amplitudina A cos  x. Piirrä värähtelyn kuvaaja sekä samaan kuvioon amplitudikäyrän
kuvaaja.
x. Piirrä värähtelyn kuvaaja sekä samaan kuvioon amplitudikäyrän
kuvaaja.
Tehtävä 136
Piirrä funktion y = sin 10x + sin 9x kuvaaja. Piirrä myös funktion y = 2 cos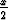 kuvaaja samaan kuvioon. Miten em. funktiot suhtautuvat toisiinsa? Laske yhteys
trigonometrisesti.
kuvaaja samaan kuvioon. Miten em. funktiot suhtautuvat toisiinsa? Laske yhteys
trigonometrisesti.
Tehtävä 137
Kaksi eritaajuista, mutta sama-amplitudista sinivärähtelyä yhdistetään: y(t) = sin 10t + sin(9t + /2). Saata värähtely muotoon y(t) = A cos(
/2). Saata värähtely muotoon y(t) = A cos( 1t +
1t +  1) sin(
1) sin( 2t +
2t +  2).
Piirrä värähtelyn kuvaaja. Mikä tulkinta voidaan antaa yhdistetyn värähtelyn tekijälle
A cos (
2).
Piirrä värähtelyn kuvaaja. Mikä tulkinta voidaan antaa yhdistetyn värähtelyn tekijälle
A cos ( 1 t +
1 t +  1)?
1)?
Tehtävä 138
Osoita, että y = sin 2x - esittää harmonista värähtelyä. Määritä amplitudi,
frekvenssi ja vaihe.
esittää harmonista värähtelyä. Määritä amplitudi,
frekvenssi ja vaihe.
Tehtävä 139
Vaihtovirran kolmen eri vaiheen jännitteet ovat sama-amplitudisia ja samataajuisia sinivärähtelyjä, joiden vaihe-ero on 2 /3:
/3:
Vi (t) = V0 sin( t +
t +  i), i = 1, 2, 3;
i), i = 1, 2, 3;  2 =
2 =  1 +
1 + 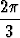 ,
,  3 =
3 =  1 +
1 + 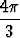 .
.
Mikä on jännitteiden summa?
Tehtävä 140
Määritä harmonisen värähtelyn
y = sin  x + 2 sin(
x + 2 sin( x +
x + 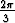 ) + 3 sin(
) + 3 sin( x +
x + 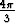 )
)
amplitudi ja vaihekulma. Piirrä komponenttivärähtelyjen ja summan kuvaajat.
Tehtävä 141
Määritä värähtelyn y = A sin x + A sin(
x + A sin( x +
x +  ) amplitudi, kun vaihe-ero on
a)
) amplitudi, kun vaihe-ero on
a)  =
=  /2, b)
/2, b)  =
=  , c)
, c)  = 2
= 2 .
.
Tehtävä 142
Mikä on värähtelyn sin 5x + sin 7x amplitudikäyrän jakso? Montako värähdystä mahtuu jaksolle? Mikä on värähtelyn jakso? Piirrä kuvio.4.7 Trigonometristen funktioiden käänteisfunktiot
Tehtävä 143
Laske tarkat arvot lausekkeille
a) sin(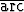 cos (-
cos (-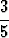 )), b) cos(
)), b) cos(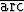 sin(-
sin(-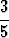 )), c) sin(
)), c) sin(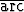 tan(-
tan(-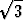 )), d) sin(
)), d) sin(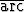 cot(-
cot(-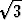 )).
)).
Tehtävä 144
Laske tarkat arvot lausekkeille
a) sin(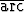 tan 2 -
tan 2 - 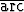 tan 3), b) cos(
tan 3), b) cos(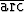 cot
cot 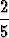 +
+ 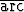 tan
tan 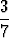 ), c) tan(
), c) tan(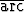 sin
sin 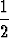 -
- 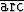 cos
cos 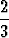 ).
).
Tehtävä 145
Mitä arvoja lauseke arccos(cos 13 /4) voi saada?
/4) voi saada?
Tehtävä 146
Ratkaise yhtälöt a)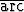 tan x =
tan x =  /4 -
/4 - 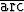 tan 3, b)
tan 3, b) 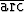 cos x =
cos x = 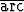 tan 1 +
tan 1 + 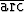 cos(-3/4).
cos(-3/4).
Tehtävä 147
Piirrä käyrä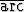 tan x +
tan x + 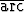 tan y =
tan y =  /4.
/4.
Tehtävä 148
Määritä harmonisten värähtelyjen| a) | y = sin x + sin(x - 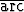 tan tan 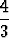 ), ), | ||
| b) | y = 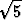 sin( sin( x + x + 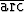 tan tan 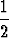 ) + 2 ) + 2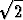 sin( sin( x + x + 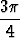 ) + ) + 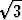 sin( sin( x - x -  ) ) |
amplitudi ja vaihekulma. Piirrä kuvaajat.
Tehtävä 149
Lisäämällä harmoniseen värähtelyyn y1 = 2 sin( x +
x + 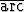 tan 2
tan 2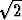 ) sopivasti
valittu harmoninen värähtely y2, jonka kulmataajuus on myös
) sopivasti
valittu harmoninen värähtely y2, jonka kulmataajuus on myös  , saadaan summaksi
värähtely y = 6 sin
, saadaan summaksi
värähtely y = 6 sin  x. Mikä on värähtelyn y2 amplitudi?
x. Mikä on värähtelyn y2 amplitudi?
Tehtävä 150
Sievennä seuraavat lausekkeet ja piirrä kuvaajat:a) y = 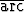 tan(tan x), tan(tan x), | b) y = 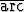 tan tan 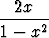 , , | ||||||
c) y = 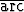 tan tan 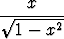 , , | d) y = sin(2 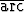 tan x), tan x), | ||||||
e) y = y = 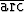 tan x + tan x + 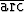 tan tan 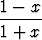 , , | f) y = 2 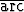 tan x + tan x + 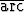 sin sin  . . |
Tehtävä 151
Tutki graafisesti kaavan
2 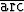 sin x =
sin x = 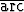 cos(1 - 2x2)
cos(1 - 2x2)
voimassaoloa. Millä muuttujan arvoilla funktiot ovat määriteltyjä?
Tehtävä 152
Tutki kaavan
2 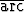 sin x =
sin x = 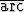 cos(1 - 2x2)
cos(1 - 2x2)
voimassaoloa käyttäen sijoitusta x = sin t, -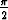 < t <
< t < 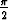 .
.
Tehtävä 153
Tutki kaavan
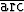 tan x +
tan x + 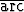 tan y =
tan y = 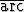 tan
tan 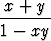 , xy
, xy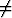 1,
1,
voimassaoloa. Siirrä kaavassa kaikki termit samalle puolen yhtäläisyysmerkkiä ja piirrä vastaava pinta z = f(x, y).
4.8 Hyperboliset funktiot
Tehtävä 154
Osoita, että hyperbolisille funktioille pätee kaava(cosh x + sinh x)n = cosh nx + sinh nx.
Millainen luku voi n olla?
Tehtävä 155
Osoita, että yhtälöllä cos x cosh x + 1 = 0 on äärettömän monta reaalijuurta.4.9 Hyperbolisia kaavoja
Tehtävä 156
Johda kaavat, joissa sinh(x/2) ja cosh(x/2) lausutaan funktion cosh x avulla.Tehtävä 157
Johda hyperbolisille funktioille kaavat| sinh x + sinh y = . . . , | sinh x - sinh y = . . . , | ||||||
| cosh x + cosh y = . . . , | cosh x - cosh y = . . . |
samalla tavoin kuin vastaavat kaavat johdetaan trigonometrisille funktioille. Onko kaavoissa merkkieroja?
4.10 Hyperbolisten funktioiden käänteisfunktiot
Tehtävä 158
Laske logaritmin avulla tarkka arvo lausekkeelle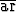 cosh
cosh 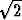 .
.
Tehtävä 159
Laske tarkat arvot funktioille cosh x ja tanh x, kun x = arsinh .
.
Tehtävä 160
Osoita, että
arcosh x = ln(x ± 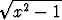 ) = ± ln(x +
) = ± ln(x + 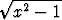 ).
).
Millä arvoilla x 
 kaava on pätevä?
kaava on pätevä?
Tehtävä 161
Millä arvoilla funktio f(x) =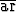 cosh(coth(ln x)) on määritelty? Sievennä
funktion lauseke ja piirrä sen kuvaaja.
cosh(coth(ln x)) on määritelty? Sievennä
funktion lauseke ja piirrä sen kuvaaja.
Tehtävä 162
Lausu funktio f(x) = arsinh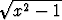 logaritmifunktion avulla. Millä
muuttujan reaaliarvoilla funktio on määritelty? Miten funktio suhtautuu funktioon
logaritmifunktion avulla. Millä
muuttujan reaaliarvoilla funktio on määritelty? Miten funktio suhtautuu funktioon
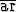 coshx? Piirrä funktion kuvaaja.
coshx? Piirrä funktion kuvaaja.
Tehtävä 163
Sievennä lausekkeet a) tanh(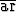 cosh x), b) artanh
cosh x), b) artanh 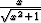 .
.